pembahasan selanjutnya adalah
- trigonometri,
- dimensi tiga,
- suku banyak,
- integral, serta
- permutasi dan kombinasi.
Soal No. 11 tentang Trigonometri
A. 1 − (𝑎2 − 1)2
B. 1 − 2(𝑎2 − 1)2
C. 1 + 2(𝑎2 − 1)2
D. 1 − ½(𝑎2 − 1)2
E. 1 + ½(𝑎2 − 1)2
Pembahasan
Kedua ruas pada data yang diketahui kita kuadratkan terlebih dahulu.
(sin 𝑥 + cos 𝑥)2 = 𝑎2
sin2 𝑥 + cos2 𝑥 + 2 sin 𝑥 cos 𝑥 = 𝑎2
1 + 2 sin 𝑥 cos 𝑥 = 𝑎2
2 sin 𝑥 cos 𝑥 = 𝑎2 − 1
sin 𝑥 cos 𝑥 = ½(𝑎2 − 1) …(1)
Selanjutnya, kita langsung bisa masuk ke pertanyaan:
sin4𝑥 + cos4𝑥
= (sin2𝑥)2 + (cos2𝑥)2
= (sin2𝑥 + cos2𝑥)2 − 2 sin2 𝑥 cos2 𝑥
= 12 − 2 sin2 𝑥 cos2 𝑥
= 1 − 2[½(𝑎2 − 1]2
= 1 − 2 . ¼(𝑎2 − 1]2
= 1 − ½(𝑎2 − 1)2
Jadi, nilai dari sin4 𝑥 + cos4 𝑥 adalah 1 − ½(𝑎2 − 1)2 (D).
Soal No 12 tentang Dimensi Tiga
A. ⅙
B. ¼
C. ⅓
D. ⅔
E. ½

Pembahasan
Perhatikan gambar ilustrasi untuk soal di atas!

Anggap panjang sisi kubus tersebut adalah a. Volume kubus ABCD.EFGH (Vk) adalah:
Vk = s3
= a3
Luas alas PQRS (La) adalah:
La = ½ × d1 × d2
= ½ × PS × QR
= ½ × a × a
= ½𝑎2
Volume limas T.PQRS (Vl) adalah:
Vl = ⅓ × La × t
= ⅓ × ½𝑎2 × a
= ⅙ 𝑎3
= ⅙ Vk
Jadi, volume limas E.PQRS adalah ⅙ volume kubus ABC.EFGH (A).
Soal No. 13 tentang Suku Banyak
A. 𝑥 + 2
B. 2𝑥
C. 𝑥
D. 1
E. 2
Pembahasan
Menurut teorema sisa:
“Jika suku banyak f(x) dibagi x − a maka sisanya adalah f(a)”.
Berdasarkan teorema sisa tersebut, jika suku banyak 𝑃(𝑥 + 1) dan 𝑃(𝑥 − 1) dibagi 𝑥 − 1 bersisa 2 maka untuk x = 1 pada 𝑃(𝑥 + 1) dan 𝑃(𝑥 − 1) akan menghasilkan 2.
𝑃(1 + 1) = 2
𝑃(2) = 2 …(1)
𝑃(1 − 1) = 2
𝑃(0) = 2 … (2)
Nah, jika 𝑃(𝑥) dibagi 𝑥2 − 2𝑥 sisanya adalah ax + b (pembagi berderajat 2, sisa berderajat 1). Sedangkan pembaginya dapat difaktorkan menjadi:
𝑥2 − 2𝑥 = x(x − 2)
= (x − 0)(x − 2)
Karena x − 0 dan x − 2 faktor dari 𝑥2 − 2𝑥, maka:
P(x) dibagi x − 0 bersisa ax + b
P(0) = a.0 + b
2 = b
b = 2
P(x) dibagi x − 2 bersisa ax + b
P(2) = a.2 + b
2 = 2a + 2
2a = 0
a = 0
Dengan demikian, sisa pembagian suku banyak tersebut adalah:
ax + b = 0.x + 2
= 2
Jadi, sisa pembagian suku banyak P(x) oleh 𝑥2 − 2𝑥 adalah 2 (E).
Soal No. 14 tentang Integral

Jika titik P(xo, 0) sehingga A(xo) ∶ A(1) = 1 ∶ 8 maka perbandingan luas trapesium ABPQ : DCPQ = ….
A. 2 : 1
B. 3 : 1
C. 6 : 1
D. 8 : 1
E. 9 : 1
Pembahasan
𝐴(𝑡) menyatakan luas daerah di bawah kurva 𝑦 = 𝑏𝑥2, 0 ≤ 𝑥 ≤ 𝑡. Berarti:
𝐴(𝑡) = o∫t 𝑏𝑥2dx
𝐴(xo) = o∫xo 𝑏𝑥2dx
𝐴(1) = o∫1 𝑏𝑥2dx
Selanjutnya kita tentukan nilai xo.
A(xo) ∶ A(1) = 1 ∶ 8

Perhatian gambar trapesium ABPQ : DCPQ berikut ini!

Perbandingan luas trapesium ABPQ dan DCPQ adalah:
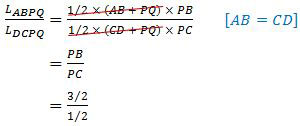
= 3/1
Jadi, perbandingan luas trapesium ABPQ dan DCPQ adalah 3 : 1 (B).
Soal No. 15 tentang Permutasi dan Kombinasi
A. 6
B. 20
C. 22
D. 40
E. 120
Pembahasan
Dari 6 rasa es krim yang tersedia, dibeli 5 es krim dengan 3 rasa berbeda. Kemungkinannya adalah:
3 es krim rasa berbeda dan 2 es krim rasa sama:
6C3 . 3C1 = 20 × 3
= 60
3 es krim rasa berbeda dan 2 es krim rasa berbeda:
6C3 . 3C2 = 20 × 3
= 60
Banyak semua kemungkinan memilih 5 es krim dengan 3 rasa berbeda adalah:
60 + 60 = 120
Jadi, banyak cara seorang pembeli dapat memilih 5 es krim dengan 3 rasa berbeda adalah 120 cara (E).
Simak Pembahasan Soal TKD Saintek SBMPTN 2014 selengkapnya.
Simak juga:
Pembahasan Matematika SBMPTN 2015
Pembahasan Matematika SBMPTN 2016
Pembahasan Matematika SBMPTN 2017
Pembahasan Matematika SBMPTN 2018
Pembahasan Matematika UTBK SBMPTN 2019
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
