pembahasan selanjutnya adalah

Pembahasan soal Matematika Saintek Tes Kompetensi Akademik Sains dan Teknologi (TKA Saintek) pada Ujian Tulis Berbasis Komputer (UTBK) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2019 nomor 11 sampai dengan nomor 15 tentang:
- barisan dan deret,
- lingkaran,
- vektor,
- integral. dan
- transformasi geometri.
Soal No. 11 tentang Barisan dan Deret
| A. | 1590 |
| B. | 1596 |
| C. | 1600 |
| D. | 1690 |
| E. | 1700 |
Pembahasan
Jumlah 5 suku pertama adalah 100.
| U1 + U2 + U3 + U4 + U5 | = | 100 |
| a + 3a + 5a + 7a + 9a | = | 100 |
| 25a | = | 100 |
| a | = | 4 |
Beda barisan tersebut adalah:
Untuk mencari nilai U2 + U3 + U4 + U5 + ⋯ + U20 sebaiknya kita gunakan rumus.
Sn = ½ n[2a + (n − 1)b]
Deret tersebut dimulai dari U2 dan berakhir di U20. Hitungannya sama saja dengan S20 dikurangi U1.
| S20 − U1 | = | ½ ∙ n[2a + 19 ∙ b] − a |
| = | ½ ∙ 20[2 ∙ 4 + 19 ∙8] − 4 | |
| = | 10(8 + 152) − 4 | |
| = | 1600 − 4 | |
| = | 1596 |
Jadi, nilai dari U2 + U3 + U4 + U5 + ⋯ + U20 adalah 1596 (B).
Soal No. 12 tentang Lingkaran
| A. | −1 < a < 3 |
| B. | −3 < a < −1 |
| C. | 3 < a < 5 |
| D. | 1 < a < 3 |
| E. | −3 < a < 5 |
Pembahasan
Karena titik P(4, a) berada di dalam lingkaran maka substitusi titik P ke persamaan lingkaran akan menghasilkan pertidaksamaan “
| x2 + y2 − 8x − 2y + 1 | = | |
| 42 + a2 − 8∙4 − 2∙a + 1 | < | |
| 16 + a2 − 32 − 2a + 1 | < | |
| a2 − 2a − 15 | < | |
| a2 + 3a − 5 | < |
Pembuat nol pertidaksamaan di atas adalah:
a = −3 atau a = 5
Karena tanda pertidaksamaannya “<” maka daerah penyelesaiannya berada di antara pembuat nol.
−3 < a < 5
Jadi, nila a yang mungkin adalah −3 < a < 5 (E).
Soal No. 13 tentang Vektor
| A. | x ≤ −1 |
| B. | −2 ≤ x ≤ 1 |
| C. | −1 ≤ x ≤ 2 |
| D. | x > 2 |
| E. | x > 1 |

Pembahasan
Panjang proyeksi vektor b ke a adalah:

Sementara itu diketahui bahwa:

Sehingga diperoleh:

Pembuat nol pertidaksamaan di atas adalah:
x = −1 dan x = 2
Karena tanda pertidaksamaannya “≤” maka hasil dari pertidaksamaan tersebut berada di antara pembuat nol.
−1 ≤ x ≤ 2
Jadi, nilai x yang memenuhi adalah −1 ≤ x ≤ 2 (C).
Soal No. 14 tentang Integral
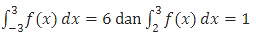
maka nilai dari
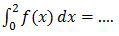
Pembahasan
Fungsi yang memenuhi f(x) = f(−x) adalah fungsi genap. Kaidah yang berlaku untuk integral fungsi genap adalah sebagai berikut:
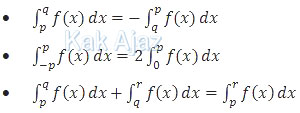
Ok, mari kita kerjakan dengan menyederhanakan data yang diketahui pada soal!
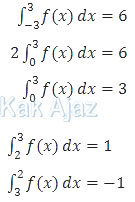
Dengan demikian,
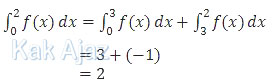
Jadi, nilai dari integral tersebut adalah 2 (B).
Soal No. 15 tentang Transformasi Geometri
| A. | −3 |
| B. | −1/2 |
| C. | 1/2 |
| D. | 3 |
| E. | 4 |
Pembahasan
Misal titik A(x, y) digeser sejauh a satuan ke kanan dan b satuan ke bawah.
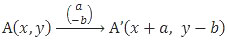
Kemudian titik A’ dicerminkan terhadap sumbu x.
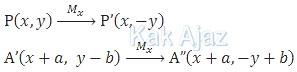
Diperoleh:
| x’ = x + a | → | x = x’ − a |
| y’ = −y + b | → | y = y’ + b |
Dengan demikian bayangan dari garis y = 2x + 1 adalah:
| y | = | 2x + 1 |
| y’ + b | = | 2(x’ − a) + 1 |
| y’ | = | 2x’ − 2a + 1 − b |
Jika disandingkan dengan bayangan yang disebutkan dalam soal maka:
| y | = | ax + b |
| y | = | 2x − 2a + 1 − b |
Diperoleh:
| a | = | 2 |
| b | = | −2a + 1 − b |
| 2b | = | −2a + 1 |
| 2b | = | −2∙2 + 1 |
| 2b | = | −3 |
| b | = | −3/2 |
Sehingga,
Jadi, nilai dari a + b adalah 1/2 (C).
Simak Pembahasan Soal TKA Saintek UTBK SBMPTN 2019 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
