Pembahasan Matematika No. 1 – 5 TKD Saintek SBMPTN 2018 Kode Naskah 466

Pembahasan soal Matematika Tes Kemampuan Dasar Sains dan Teknologi (TKD Saintek) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2018 Kode Naskah 466 nomor 1 sampai dengan nomor 5 tentang:

• fungsi trigonometri, 
• transformasi geometri, 
• dimensi tiga, 
• limit fungsi, serta 
• barisan dan deret.

Soal No. 1 tentang Fungsi Trigonometri

Pembahasan

Diketahui:

f(x)_max = 7
f(x)_min = 3

Nilai maksimum atau minimum fungsi trigonometri bergantung pada amplitudo (k) dan nilai konstanta (c).

Nilai maksimum terjadi saat amplitudonya positif.

      f(x) = k sin⁡(x) + c
f(x)_max = +k + c
         7 = +k + c           … (1)

Sedangkan nilai minimum terjadi saat amplitudonya negatif.

f(x)_min = −k + c
         3 = −k + c           … (2)

Selanjutnya kita eliminasi persamaan (1) dan (2).

7 = +k + c
3 = −k + c
⎯⎯⎯⎯⎯⎯⎯  −
4 = 2k
k = 2

Kemudian kita substitusi k = 2 ke persamaan (1).

7 = k + c
7 = 2 + c
c = 5

Dengan modal nilai k dan c yang baru saja kita peroleh, mari kita tentukan nilai maksimum dari fungsi g(x).

      g(x) = 2k cos⁡(x) + 5c
g(x)_max = 2k + 5c 
             = 2 ∙ 2 + 5 ∙ 5
             = 4 + 25
             = 29

Jadi, nilai maksimum fungsi g(x) adalah 29 (E).

Soal No. 2 tentang Transformasi Geometri

Pembahasan

Gradien garis melalui titik O(0, 0) dan P(a, b) adalah 2.

Pencerminan terhadap sumbu y dirumuskan:

Sehingga,

Kemudian hasil pencerminan tersebut digeser 1 satuan ke atas dan 4 satuan ke kiri. Ini berarti bahwa nilai absis (x) dikurangi 4 sedangkan nilai ordinat (y) ditambah 1.

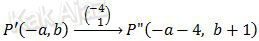
Gradien garis yang melalui titik O(0,0) dan titik P”(−a − 4, b + 1) adalah −1.

Substitusi persamaan (1) ke persamaan (2) diperoleh:

a − 2a = −3
      −a = −3
        a = 3

Substitusi a = 3 ke persamaan (1) diperoleh:

b = 2a
   = 2 ∙ 3
   = 6

Jadi, koordinat titik P(a, b) adalah P(3, 6) (E).

Soal No. 3 tentang Dimensi Tiga

Pembahasan

Kubus yang dimaksud pada soal adalah:

Jarak titik H ke garis PQ adalah garis HR. Garis HR merupakan sisi tegak segitiga siku-siku HRQ. Oleh karena itu, kita perlu mencari panjang HQ dan RQ.

Pandang garis HQ pada kubus. Untuk menempuh jarak terdekat HQ pada kubus bisa melalui HG – GC – CQ. Sehingga:

HQ² = HG² + GC² + CQ²
        = (2√2)² + (2√2)² + (√2)²
        = 8 + 8 + 2
        = 18

Sedangkan PQ merupakan sisi miring segitiga PBQ, sehingga:

PQ = √(PB² + BQ²)
      = √[(√2)² + (√2)²]
      = √4
      = 2

Panjang RQ adalah setengah dari panjang PQ.

RQ = ½ × 2
       = 1

Dengan demikian, panjang HR adalah:

HR = √(HQ² − RQ²)
       = √(18 − 1)
       = √17

Jadi, jarak antara titik H dengan garis PQ adalah √17 cm (C).

Soal No. 4 tentang Limit Fungsi

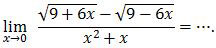
A.   0
B.   1
C.   2
D.   3
E.   4

Pembahasan

Limit fungsi bentuk pecahan di atas lebih mudah diselesaikan dengan Dalil L’Hopital. Caranya dengan menurunkan pembilang dan penyebutnya.

Turunan pembilang:

Turunan penyebut:

y = x² + x
y’ = 2x + 1

Dengan demikian,

Dengan melakukan substitusi x = 0, diperoleh:

Jadi, nilai limit fungsi tersebut adalah 2 (C).

Soal No. 5 tentang Barisan dan Deret

Pembahasan

Suku ke-n deret geometri dirumuskan:

u_n = arⁿ⁻¹

Berdasarkan rumus di atas, mari kita ulas data-data pada soal di atas. Kak Ajaz mulai dari data yang pertama.

     u₃ + u₄ = 4(u₁ + u₂)
  ar² + ar³ = 4(a + ar)
r² (a + ar) = 4(a + ar)
              r² = 4
                r = ±2

Selanjutnya, kita ulas data yang kedua.

  u₁u₄ = 4u₂
a ∙ ar³ = 4ar
     ar² = 4

Substitusi r² = diperoleh:

a ∙ 4 = 4
     a = 1

Nah, sekarang kita cari jumlah 4 suku pertama deret tersebut untuk r = 2 dan r = −2.

Untuk r = 2

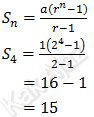
Untuk r = −2

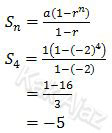
Jadi, jumlah 4 suku pertama yang mungkin adalah 15 (E).

Simak Pembahasan Soal TKD Saintek SBMPTN 2018 selengkapnya.

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih