pembahasan selanjutnya adalah
- lingkaran,
- trigonometri,
- vektor,
- transformasi geometri, dan
- dimensi tiga.
Soal No. 1 tentang Lingkaran
x2 + y2 − 6x − 2y + k = 0
sehingga garis singgung lingkaran di titik A dan B berpotongan di C(8, 1). Jika luas segiempat yang melalui A, B, C, dan pusat lingkaran adalah 12 maka k = ….
A. −1
B. 0
C. 1
D. 2
E. 3
Pembahasan
Bentuk umum persamaan lingkaranx2 + y2 − 6x − 2y + k = 0 adalah x2 + y2 + Ax + By + C = 0.Berdasarkan bentuk umum ini diperoleh:
A = −6
B = −2
C = k
pusat lingkaran: (−½A, −½B)
(−½×(−6), −½×(−2))
(3, 1)
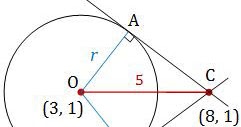
Gambar ilustrasi untuk soal di atas adalah:

Luas segiempat OACB = 12 sehingga luas segitiga AOC = 6. Sedangkan segitiga AOC adalah segitiga siku-siku dengan panjang sisi miring = 5. Dengan demikian dapat dipastikan panjang sisi OA = 3 dan sisi AC = 4 (triple Pythagoras).
Nah, kita sudah mendapatkan nilai jari-jari lingkaran tersebut, yaitu r = OA = 3. Sekarang kita gunakan rumus jari-jari lingkaran untuk mendapatkan nilai k.
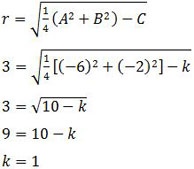
Jadi, nilai k pada persamaan lingkaran tersebut adalah 1 (C).
Soal No. 2 tentang Trigonometri
maka tan(3x + 75°) tan(x + 15°) = ….
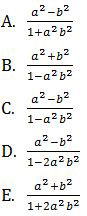

Pembahasan
Kita buat permisalan dulu agar tampak lebih sederhana.
Misal: A = 2x + 45° → tan A = a
B = x + 30° → tan B = b
Sehingga: A + B = 3x + 75°
A − B = x + 15°
Sekarang kita masuk ke bagian pertanyaan:

Dengan demikian, dengan menggunakan rumus (a + b)(a − b) = a2 − b2, diperoleh:
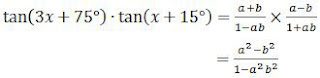
Jadi, nilai tan(3x + 75°) tan(x + 15°) adalah opsi (C).
Soal No. 3 tentang Vektor
A. t < −1 atau t > 3
B. t < −3 atau t > 1
C. −3 < t < 1
D. −1 < t < 3
E. 1 < t < 3
Pembahasan
Panjang vektor proyeksi OA terhadap OB kurang dari 4/√5:

t2 + 2t + 1 < 4
t2 + 2t − 3 < 0
(t + 3)(t − 1) < 0
Karena koefisien t2 positif maka tanda pertidaksamaan “<” mempunyai daerah penyelesaian di antara t = −3 dan t = 1. Diperoleh:
−3 < t < 1
Jadi, nilai t yang mungkin adalah −3 < t < 1 (C).
Soal No. 4 tentang Transformasi Geometri
A. y = x + 4
B. y = −x + 4
C. y = x + 2
D. y = x − 2
E. y = −x − 4
Pembahasan
Pencerminan terhadap garis y = k dirumuskan sebagai:
P(x, y) —→ P'(x, 2k − y)
Sehingga diperoleh:
x’ = x
y’ = 2k − y (k = 3)
= 2×3 − y
= 6 − y
Dengan demikian, hasil pencerminan garis y = −x + 2 adalah:
y’ = −x’ + 2
6 − y = −x + 2
−y = −x − 4
y = x + 4
Jadi, pencerminan garis y = −x + 2 terhadap garis y = 3 menghasilkan garis y = x + 4 (A).
Soal No. 5 tentang Dimensi Tiga
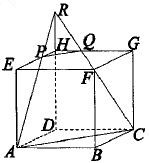
Jika panjang rusuk kubus adalah 6 maka volume ACD.PQH adalah ….
A. 46
B. 52
C. 54
D. 76
E. 81
Pembahasan
Perhatikan segitiga DCR!

Segitiga CDR sebangun dengan segitiga HQR sehingga diperoleh perbandingan:

6x = 24 + 4x
2x = 24
x = 12
Volume bangun ACD.PQH merupakan pengurangan dari volume limas R.ACD dengan limas R.PQH. Mari kita tentukan volume masing-masing limas tersebut!
Volume limas R.ACD (V1)
V1 = ⅓ × La × t
= ⅓ × L ΔACD × DR
= ⅓ × ½ . 6 . 6 × 18
= 108
Volume limas R.PQH (V2)
V2 = ⅓ × La × t
= ⅓ × L ΔPQH × HR
= ⅓ × ½ . 4 . 4 × 12
= 32
Dengan demikian, volume ACD.PQH adalah:
V = V1 − V2
= 108 − 32
= 76
Jadi, volume bangun ruang ACD.PQH adalah 76 satuan volume (D).
Simak Pembahasan Soal TKD Saintek SBMPTN 2015 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat