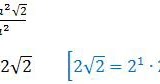pembahasan selanjutnya adalah
- barisan dan deret,
- vektor,
- suku banyak,
- matriks, serta
- pertidaksamaan logaritma.
Soal No. 1 tentang Barisan dan Deret
A. −2
B. −√2
C. 2
D. 2√2
E. 4
Pembahasan
Rasio deret geometri bisa kita dapatkan dengan membandingkan suku-suku yang diketahui. Kita pilih suku ke-5 dan ke-8 karena keduanya mengandung a2 sehingga jika dibandingkan nilai a2 akan saling meniadakan.
Un = arn−1

r3 = −23/2
(r3)1/3 = −(23/2)1/3
r = −21/2
= −√2
Jadi, rasio barisan tersebut adalah −√2 (B).
Soal No. 2 tentang Vektor
A. u ∙ v = |w|
B. w = (2u + 3v)/5
C. |u − w| = |v|
D. u − v tegak lurus w
E. u + v tegak lurus w

Pembahasan
Persamaan dalam bentuk harga mutlak akan lebih mudah dikerjakan jika dilakukan pengkuadratan kedua ruas.
|v − w|2 = |u − w|2
|v|2 − 2vw
Karena |u| = |v| maka persamaan tersebut menjadi:
−2vw = −2uw
vw = uw
0 = uw − vw
uw − vw = 0
(u − v) . w = 0
Persamaan yang terakhir ini berarti perkalian dot antara vektor (u − v) dan vektor w menghasilkan nol. Sedangkan dua vektor yang dikalikan menghasilkan nol berarti kedua vektor tersebut saling tegak lurus. Dengan demikian,
u − v tegak lurus w
Jadi, pernyataan yang benar adalah opsi (D).
Soal No. 3 tentang Suku Banyak
A. 2
B. 3
C. 4
D. 6
E. 9
Pembahasan
Banyaknya akar suku banyak berderajat 9 adalah 9. Tetapi, kesembilan akar tersebut belum tentu semuanya akar real. Mungkin terdapat akar imajiner.
Akar real terjadi saat suatu fungsi bernilai nol.
f(t) = 0
t9 − t = 0
t(t8 − 1) = 0
t = 0 atau t8 − 1 = 0
t8 = 1
t = ±1
Sehingga akar-akar realnya adalah −1, 0, dan 1.
Jadi, banyak akar real dari adalah 3 (B).
Soal No. 4 tentang Matriks
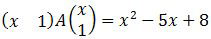
maka matriks A yang mungkin adalah ….
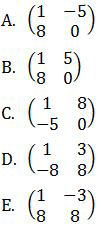
Pembahasan
Kita misalkan,
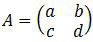
Sehingga persamaan matriks di atas menjadi:
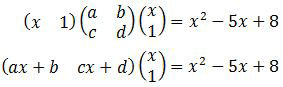
(ax + b)x + cx + d = x2 − 5x + 8
ax2 + (b + c)x + d = x2− 5x + 8
Dengan membandingkan bentuk kuadrat ruas kiri dan kanan diperoleh:
a = 1
b + c = −5
d = 8
Untuk sementara, matriks A adalah:
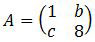
Dengan matriks A sementara ini, opsi jawaban yang mungkin adalah opsi D dan E. Sedangkan yang memenuhi b + c = −5 adalah opsi D.
Jadi, matriks A yang mungkin adalah opsi (D).
Soal No. 5 tentang Pertidaksamaan Logaritma
(1−|x|)log (3x − 1) < 1
adalah ….
A. ⅓ < x < ½
B. ⅓ < x < ⅔
C. ⅓ < x < 1
D. ½ < x < ⅔
E. ½ < x < 1
Pembahasan
Sebelum menyelesaikan pertidaksamaan logaritma, kita perhatikan dulu syarat-syarat yang berlaku.
- Bilangan pokok harus positif tetapi tidak boleh 1.
1 − |x| > 0
−|x| > −1
|x| < 1
−1 < x < 1 … (1)
1 − |x| ≠ 1
−|x| ≠ 0
|x| ≠ 0 … (2)
- Bilangan logaritma harus positif.
3x − 1 > 0
3x > 1
x > ⅓ … (3)
Sekarang kita selesaikan pertidaksamaan logaritma di atas.
(1−|x|)log (3x − 1) < 1
(1−|x|)log (3x − 1) < (1−|x|)log (1 − |x|)
Karena bilangan pokoknya antara 0 dan 1 maka tanda pertidaksamaan harus dibalik.
3x − 1 > 1 − |x|
|x| > −3x + 2
|x|2 > (−3x + 2)2
x2 > 9x2 − 12x + 4
−8x2 + 12x − 4 > 0
2x2 − 3x + 1 < 0
(2x − 1)(x − 1) < 0
Pembuat nol pertidaksamaan tersebut adalah:
2x − 1 = 0
2x = 1
x = ½
x − 1 = 0
x = 1
Karena koefisien dari x2 berharga positif maka tanda “<” berarti penyelesaian pertidaksamaan tersebut berada di antara pembuat nol.
½ < x < 1
Penyelesaian pertidaksamaan logaritma ini telah memenuhi syarat logaritma (1), (2), dan (3) sehingga tidak perlu dibuat garis bilangan untuk mencari irisan penyelesaiannya.
Jadi, penyelesaian pertidaksamaan tersebut adalah ½ < x < 1 (E).
Simak Pembahasan Soal TKD Saintek SBMPTN 2014 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat