pembahasan selanjutnya adalah

Pembahasan soal Ujian Nasional (UN) tahun 2019 bidang studi Matematika SMA-IPS nomor 11 sampai dengan nomor 15 tentang:
- aplikasi komposisi fungsi,
- invers fungsi,
- fungsi kuadrat,
- suku ke-n deret aritmetika, dan
- jumlah n suku deret aritmetika.
Soal No. 11 tentang Aplikasi Komposisi Fungsi
A. 38 pakaian
B. 41 pakaian
C. 42 pakaian
D. 46 pakaian
E. 47 pakaian
Pembahasan
Cara 1 (Tahapan Fungsi)
Banyak pola yang diperoleh dari 100 m2 kain adalah:
f(x) = 3/4 x + 5
f(100) = 3/4 × 100 + 5
= 75 + 5
= 80
Banyaknya pakaian yang dihasilkan dari 80 pola adalah:
g(x) = 1/2 x + 6
g(80) = 1/2 × 80 + 6
= 40 + 6
= 46
Cara 2 (Komposisi Fungsi)
g(x) = 1/2 x + 6
g[f(x)] = 1/2 f(x) + 6
= 1/2 (3/4 x + 5) + 6
= 3/8 x + 5/2 + 6
= 3/8 x + 17/2
g[f(100)] = 3/8 × 100 + 17/2
= 37,5 + 8,5
= 46
Jadi, banyak pakaian yang dihasilkan adalah 46 pakaian (D).
Soal No. 12 tentang Invers Fungsi
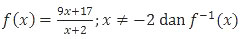
adalah invers dari f(x). Nilai dari f−1(10) adalah ….
A. −16
B. −3
C. −2
D. 2
E. 12
Pembahasan
Invers fungsi dalam bentuk pecahan linear dirumuskan sebagai:

Berpedoman pada rumus di atas maka:

Jadi, nilai dari f−1(10) adalah −3 (B).
Soal No. 13 tentang Fungsi Kuadrat
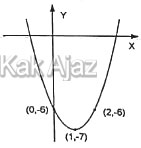
A. y = 2x2 − x − 6
B. y = 2x2 + x − 6
C. y = x2 − 2x − 6
D. y = x2 + 2x − 6
E. y = x2 − 4x − 6

Pembahasan
Persamaan grafik fungsi kuadrat yang melalui titik puncak (p, q) dirumuskan sebagai:
y = a(x − p)2 + q
Dengan titik puncak (1, −7) diperoleh:
y = a(x − 1)2 − 7 … (1)
Grafik tersebut melalui titik (0, −6). Kita substitusikan titik tersebut ke persamaan (1) untuk mendapatkan nilai a. Diperoleh:
−6 = a(0 − 1)2 − 7
−6 = a − 7
a = 1
Nah, kita substitusi a = 1 ke persamaan (1) untuk mendapatkan persamaan fungsinya.
y = 1(x − 1)2 − 7
= x2 − 2x + 1 − 7
= x2 − 2x − 6
Jadi, persamaan grafik fungsi kuadrat pada gambar di atas adalah y = x2 − 2x − 6 (C).
Soal No. 14 tentang Suku ke-n Deret Aritmetika
A. 162
B. 118
C. 110
D. 92
E. 70
Pembahasan
Cara 1
Diketahui:
U4 = 33
U7 = 54
Suku ke-n deret aritmetika dinyatakan sebagai:
Un = a + (n − 1)b
Berdasarkan rumus di atas, maka:
U4 = a + 3b = 33
U7 = a + 6b = 54
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ −
−3b = −21
b = 7
Substitusi b = 7 ke U4 untuk mendapatkan nilai a.
a + 3×7 = 33
a + 21 = 33
a = 12
Dengan demikian,
U15 = a + 14b
= 12 + 14×7
= 12 + 98
= 10
Cara 2
Diketahui:
U4 = 33
U7 = 54
(7 − 4)b = 54 − 33
3b = 21
b = 7
Suku ke-n deret aritmetika juga bisa dirumuskan:
Un = Uk + (n − k)b
Uk bisa menggunakan U4 atau U7.
U15 = U4 + (15 − 4)b
= 33 + 11×7
= 33 + 77
= 110
Jadi, Suku ke-15 barisan tersebut adalah 110 (C).
Soal No. 15 tentang Jumlah n Suku Deret Aritmetika
A. 816
B. 819
C. 826
D. 909
E. 919
Pembahasan
Diketahui:
U5 = 28
U10 = 53
Dengan cara seperti pembahasan no. 14, diperoleh:
U5 = a + 4b = 28
U10 = a + 9b = 53
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ −
−5b = −25
b = 5
Substitusi b = 5 ke U5 untuk mendapatkan nilai a.
a + 4×5 = 28
a + 20 = 28
a = 8
Jumlah n suku pertama deret aritmetika dirumuskan:
Sn = 1/2 n[2a + (n − 1)b]
S18 = 1/2×18(2×8 + 17×5)
= 9(16 + 85)
= 9×101
= 909
Jadi, jumlah 18 suku pertama barisan aritmetika tersebut adalah 909 (D).
Simak Pembahasan Soal Matematika IPS UN 2019 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
