pembahasan selanjutnya adalah

Pembahasan soal Ujian Nasional (UN) tahun 2019 bidang studi Matematika SMA-IPS nomor 1 sampai dengan nomor 5 tentang:
- sistem persamaan linear,
- model matematika sistem persamaan linear,
- persamaan matriks untuk sistem persamaan linear,
- invers matriks, dan
- kesamaan matriks.
Soal No. 1 tentang Sistem Persamaan Linear
A. 63
B. 57
C. 21
D. −27
E. −39
Pembahasan
Kita eliminasikan kedua persamaan linear tersebut.

Substitusi y = 6 ke persamaan yang kedua.
x + 4y = 15
x + 24 = 15
x = 15 − 24
x = −9
Dengan demikian,
5x1 + 3y1 = 5×(−9) + 3×6
= −45 + 18
= −27
Jadi, nilai dari 5x1 + 3y1 adalah 27 (D).
Soal No. 2 tentang Model Matematika Sistem Persamaan Linear
| A. | 10x + 15y = 185 dan x + y = 150 |
| B. | 2x + 3y = 370 dan x + y = 150 |
| C. | 3x + 2y = 370 dan x + y = 150 |
| D. | 2x + 3y = 185 dan x + y = 150 |
| E. | x + y = 370 dan 2x + 3y = 150 |
Pembahasan
Diketahui x menyatakan banyak kambing dan y menyatakan banyak sapi.
Jumlah semua hewan (kambing dan sapi) adalah 150 ekor.
x + y = 150
Biaya pakan kambing Rp10.000,00 per ekor, biaya pakan sapi Rp15.000,00 per ekor. Biaya total pakan ternak Rp1.850.000,00.
10.000x + 15.000y = 1.850.000
2x + 3y = 370 [dibagi 5.000]
Jadi, model matematika yang tepat untuk permasalahan tersebut adalah opsi (B).
Soal No. 3 tentang Persamaan Matriks untuk Sistem Persamaan Linear
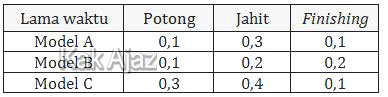
Jumlah waktu yang tersedia di bagian pemotongan, penjahitan, dan finishing disajikan dalam tabel berikut.

Jika banyak model pakaian yang akan diproduksi untuk model A, B, dan C berturut-turut x, y, dan z, persamaan matriks yang sesuai untuk masalah tersebut adalah ….


Pembahasan
Lama waktu pemotongan untuk pakaian model A, B, dan C adalah:
0,1x + 0,1y + 0,3z = 68
x + y + 3z = 680 [×10]
Lama waktu penjahitan untuk pakaian model A, B, dan C adalah:
0,3x + 0,2y + 0,4z = 116
3x + 2y + 4z = 1160 [×10]
Lama waktu penjahitan untuk pakaian model A, B, dan C adalah:
0,1x + 0,2y + 0,1z = 51
x + 2y + z = 510 [×10]
Sistem persamaan dari ketiga persamaan linear tersebut adalah:
x + y + 3z = 680
3x + 2y + 4z = 1160
x + 2y + z = 510
Jika dikonversi ke persamaan matriks maka akan menjadi:
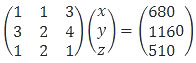
Jadi, persamaan matriks yang sesuai untuk masalah tersebut adalah opsi (D).
Soal No. 4 tentang Invers Matriks
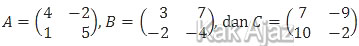
Memenuhi persamaan X = A + 2B − CT, dengan CT merupakan transpose matriks C. Invers matriks X adalah ….
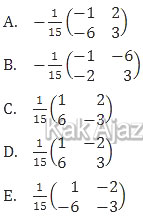
Pembahasan
Transpose matriks adalah posisi baris diganti dengan posisi kolom.
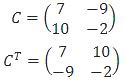
Dengan demikian, persamaan matriks di atas menjadi:
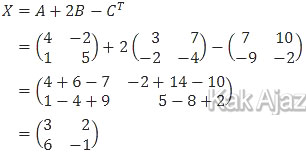
Sementara itu, invers matriks dirumuskan:

Dengan demikian,

Jadi, invers matriks X adalah opsi (C).
Soal No. 5 tentang Kesamaan Matriks
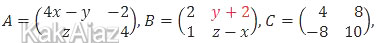
dan CT adalah transpose dari matriks C. Jika 3A − B = CT, nilai dari −3x + y + 5z adalah ….
A. 8
B. 10
C. 14
D. 16
E. 20
Catatan:
Komponen matriks B yang bercetak merah adalah salah redaksi, jangan dipergunakan dalam penghitungan.
Pembahasan
Mengenai transpose matriks bisa dilihat pada pembahasan no. 4. Sekarang kita langsung menuju ke persamaan matriksnya.
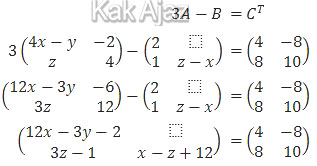
Berdasarkan kesamaan matriks di atas diperoleh:
3z − 1 = 8
3z = 9
z = 3
x − z + 12 = 10
x − 3 + 12 = 10
x + 9 = 10
x = 1
12x − 3y − 2 = 4
12 − 3y − 2 = 4
−3y + 10 = 4
−3y = −6
y = 2
Dengan demikian,
−3x + y + 5z = −3×1 + 2 + 5×3
= −3 + 2 + 15
= 14
Jadi, nilai dari −3x + y + 5z adalah 14 (C).
Simak Pembahasan Soal Matematika IPS UN 2019 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
