pembahasan selanjutnya adalah
Pembahasan soal Ujian Nasional (UN) tahun 2018 bidang studi Matematika SMA-IPS nomor 16 sampai dengan nomor 20 tentang:
- limit fungsi,
- limit fungsi aljabar,
- turunan fungsi,
- aplikasi turunan, dan
- integral tentu.
Soal No. 16 tentang Limit Fungsi
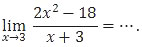
A. 4
B. 2
C. 0
D. −2
E. −4
Pembahasan
Limit di atas tidak perlu dijabarkan atau diuraikan. Langsung saja substitusikan x = 3 karena tidak menghasilkan 0/0.
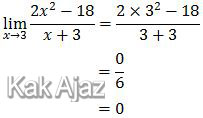
Jadi, nilai limit fungsi di atas adalah 0 (C).
Soal No. 17 tentang Limit Fungsi Aljabar

A. −3/2
B. −2/3
C. 0
D. 2/3
E. 3/2
Pembahasan
Pembilang dan penyebut fungsi di atas difaktorkan terlebih dahulu.

Jadi, nilai limit fungsi aljabar di atas adalah 3/2 (E).
Soal No. 18 tentang Turunan Fungsi
A. f’(x) = 3(5x − 3)2
B. f’(x) = 5(5x − 3)2
C. f’(x) = 8(5x − 3)2
D. f’(x) = 15(5x − 3)2
E. f’(x) = 45(5x − 3)2

Pembahasan
Fungsi yang dipangkatkan, yaitu (5x − 3), diturunkan terlebih dahulu. Setelah itu, pangkatnya diturunkan.
f(x) = (5x − 3)3
f’(x) = 5 ∙ 3(5x − 3)2
= 15(5x − 3)2
Jadi, turunan pertama fungsi tersebut adalah opsi (D).
Soal No. 19 tentang Aplikasi Turunan
A. −2 < x < 3
B. −3 < x < 2
C. 2 < x < 3
D. x < −2 atau x > 3
E. x < −3 atau x > 2
Pembahasan
Fungsi f(x) akan turun jika turunan fungsi tersebut kurang dari nol.
f(x) = 1/3 x3 − 1/2 x2 − 6x + 2
f’(x) < 0
x2 − x − 6 < 0
(x + 2)(x − 3) < 0
Pembuat nol: x = −2 dan x = 3
Karena tanda pertidaksamaannya “<” maka intervalnya berada di antara pembuat nol.
−2 < x < 3
Jadi, grafik fungsi tersebut turun pada interval −2 < x < 3 (A).
Soal No. 20 tentang Integral Tentu
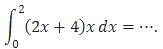
A. 13 2/3
B. 13 1/3
C. 12 1/3
D. 6 1/3
E. 1/3
Pembahasan
Sebelum diintegral, Kak Ajaz sederhanakan dulu fungsi yang akan diintegral dengan cara mengalikan.

Jadi, nilai dari integral tentu di atas adalah 13 1/3 (B).
Simak Pembahasan Soal Matematika IPS UN 2018 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat