Pembahasan Matematika IPS UN 2017 No. 6

Pembahasan soal-soal Ujian Nasional (UN) tahun 2017 bidang studi Matematika SMA-IPS nomor 6 sampai dengan nomor 10 tentang:

• fungsi kuadrat, 
• akar persamaan kuadrat, 
• persamaan kuadrat baru, 
• penerapan fungsi kuadrat, dan 
• sistem persamaan linear.

Soal No. 6 tentang Fungsi Kuadrat

Perhatikan gambar!

Persamaan grafik fungsi kuadrat dari gambar tersebut adalah ….

A.   y = 4/5 x² − 4x + 3
B.   y = 5/4 x² − 5x + 3
C.   y = 4/5 x² + 4x − 3
D.   y = 5/4 x² − 5x − 3
E.   y = 5/4 x² + 5x + 3

Pembahasan

Grafik fungsi kuadrat di atas mempunyai puncak (2, −2) dan melalui titik (0, 3).

Persamaan grafik fungsi kuadrat yang mempunyai puncak (p, q) dirumuskan sebagai:

y = a(x − p)² + q

Nah, sekarang kita substitusikan titik puncak pada rumus tersebut.

y = a(x − 2)² − 2           … (1)
y = a(x² − 4x + 4) − 2   … (2)

Untuk mendapatkan nilai a, kita substitusi titik yang dilalui grafik, yaitu titik (0, 3), pada persamaan (1). Diperoleh:

3 = a(0 − 2)² − 2
3 = 4a − 2
5 = 4a
a = 5/4

Nilai a kita substitusikan ke persamaan (2) untuk mendapatkan persamaan grafik fungsi kuadrat yang dimaksud.

y = 5/4 (x² − 4x + 4) − 2
   = 5/4 x² − 5x + 5 − 2
   = 5/4 x² − 5x + 3

Jadi, persamaan grafik fungsi kuadrat dari gambar tersebut adalah y = 5/4 x² − 5x + 3 (B).

Soal No. 7 tentang Akar Persamaan Kuadrat

Pembahasan

Persamaan kuadrat x² + 3x − 28 = 0 kita faktor terlebih dahulu. Caranya, kita cari faktor dari −28 yang jumlahnya 3. Ya, 7 dan −4.

x² + 3x − 28 = 0
(x + 7)(x − 4) = 0
x = −7 atau x = 4

Karena x₁ < x₂ maka:

x₁ = −7
x₂ = 4

Dengan demikian,

3x₁ + 2x₂ = 3×(−7) + 2×4
                = −21 + 8
                = −13

Jadi, nilai 3x₁ + 2x₂ adalah −13 (A).

Soal No. 8 tentang Persamaan Kuadrat Baru

Pembahasan

Dari persamaan kuadrat 2x² − 6x + 7 = 0 diperoleh:

a = 2
b = −6
c = 7

Penjumlahan dan perkalian akar-akar persamaan kuadrat tersebut adalah:

x₁ + x₂ = −b/a
            = −(−6)/2
            = 3           … (1)

x₁ ∙ x₂ = c/a
           = 7/2         … (2)

Misalkan persamaan kuadrat baru yang akar-akarnya (2x₁ + 1) dan (2x₂ + 1) adalah

x² − px + q = 0

maka:

p = (2x₁ + 1) + (2x₂ + 1)
   = 2x₁ + 2x₂ + 2
   = 2(x₁ + x₂) + 2
   = 2×3 + 2   [substitusi prs 1]
   = 8

q = (2x₁ + 1) (2x₂ + 1)
   = 4x₁x₂ + 2x₁ + 2x₁ + 1
   = 4x₁x₂ + 2(x₁ + x₂) + 1
   = 4×7/2 + 2×3 + 1     [substitusi prs 2]
   = 14 + 6 + 1
   = 21

Dengan demikian, persamaan kuadrat baru tersebut adalah:

x² − px + q = 0
x² − 8x + 21 = 0

Jadi, persamaan kuadrat yang akar-akarnya (2x₁ + 1) dan (2x₂ + 1) adalah x² − 8x + 21 = 0 (C).

Soal No. 9 tentang Penerapan Fungsi Kuadrat

Pembahasan

Diketahui:

k = px
p = 90 − 3x
1 ≤ x ≤ 30

Dengan melakukan substitusi p pada k = px diperoleh fungsi kuadrat k sebagai berikut:

k = px
   = (90 − 3x)x
   = 90x − 3x²
   = −3x² + 90x

Untuk mendapatkan nilai x agar fungsi k maksimum, kita bisa menggunakan dua cara, yaitu menggunakan rumus sumbu simetri fungsi kuadrat dan memanfaatkan turunan atau diferensial.

Cara I (rumus fungsi kuadrat)

Berdasarkan fungsi kuadrat k = −3x² + 90x, diperoleh:

a = −3
b = 90
c = 0

Nilai fungsi k akan maksimum pada saat x sama dengan sumbu simetri.

x = −b/2a
   = −90/(2×(−3))
   = 15

Cara II (turunan/diferensial)

Nilai fungsi k akan maksimum pada saat turunan pertamanya sama dengan nol.

            k‘ = 0
−6x + 90 = 0
          90 = 6x
            x = 90/6
               = 15

Selanjutnya nilai x tersebut kita substitusikan ke fungsi k.

  k(x) = −3x² + 90x
k(15) = −3×15² + 90×15
         = −675 + 1350
         = 675 (dalam jutaan rupiah)

Jadi, total penjualan maksimum barang k adalah Rp675.000.000,00 (B).

Soal No. 10 tentang Sistem Persamaan Linear

Misalkan (a, b) = (a₁, b₁) adalah penyelesaian dari sistem persamaan

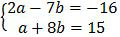
maka nilai a₁ + 2b₁ adalah ….

A.   −3
B.   −1
C.   0
D.   1
E.   3

Pembahasan

Cara yang paling umum untuk menyelesaikan sistem persamaan linear adalah eliminasi. Perhatikan eliminasi kedua persamaan linear di atas!

2a − 7b = −16  |×1|  2a − 7b  = −16
  a + 8b = 15    |×2|  2a + 16b = 30
                              ⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯  −
                                      −23b = −46
                                            b = 2

Kemudian kita substitusikan b = 2 pada salah satu persamaan linear di atas, misal persamaan linear yang kedua (karena lebih sederhana).

a + 8b = 15
a + 8×2 = 15
a + 16 = 15
        a = 15 − 16
        a = −1

Sehingga diperoleh:

a₁ = −1
b₁ = 2

Dengan demikian,

a₁ + 2b₁ = −1 + 2×2
               = −1 + 4
               = 3

Jadi, nilai a₁ + 2b₁ adalah 3 (E).

Simak Pembahasan Soal Matematika IPS UN 2017 selengkapnya.

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih