Pembahasan Matematika IPS UN 2017 No. 21

Pembahasan soal-soal Ujian Nasional (UN) tahun 2017 bidang studi Matematika SMA-IPS nomor 21 sampai dengan nomor 25 tentang:

• penerapan barisan geometri, 
• limit fungsi aljabar, 
• limit mendekati tak hingga, 
• turunan fungsi aljabar, dan 
• aplikasi turunan.

Soal No. 21 tentang Penerapan Barisan Geometri

Pembahasan

Diketahui bahwa produksi perusahaan tersebut setiap tahun turun 10% dari tahun sebelumnya. Hal ini berarti bahwa produksi tahun berikutnya adalah 90% dari tahun sebelumnya.

Karena yang ditanyakan hanya produksi tahun ketiga, maka lebih efektif diselesaikan secara manual (tanpa rumus).

Cara I (manual)

tahun I   : 9.000 unit
tahun II  : 90% × 9.000 unit = 8.100 unit
tahun III : 90% × 8.100 unit = 7.290 unit

Cara II (rumus barisan geometri)

Diketahui:

a = 9000
r = (100 − 10)%
  = 90%
  = 0,9

Produksi barang pada tahun ketiga dapat dicari dengan menggunakan rumus:

U_n = arⁿ⁻¹
U₃ = ar²
     = 9000 × 0,9²
     = 9000 × 0,81
     = 7290

Jadi, perusahaan tersebut akan memproduksi barang tersebut pada tahun ketiga sebanyak 7.200 unit (D).

Soal No. 22 tentang Limit Fungsi Aljabar

Nilai

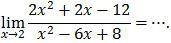
A.   −5
B.   −2
C.   0
D.   2
E.   5

Pembahasan

Ada dua cara menyelesaikan limit fungsi aljabar di atas. Cara pertama, memfaktorkan pembilang dan penyebutnya. Cara kedua, menurunkan pembilang dan menyebutnya. Setelah mengalami pemfaktoran atau penurunan, kita substitusikan x = 2.

Cara I (pemfaktoran)

Cara II (Penurunan)

Jadi, nilai limit fungsi aljabar tersebut adalah −5 (A).

Soal No. 23 tentang Limit Mendekati Tak Hingga

Nilai

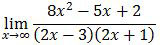
adalah ….

A.   −4
B.   −2
C.   2
D.   4
E.   8

Pembahasan

Yang perlu diperhatikan pada limit mendekati tak hingga adalah pangkat tertingginya. Oleh karena itu, pembilang pada limit fungsi di atas kita jabarkan terlebih dahulu.

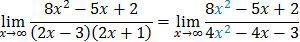
Perhatikan pangkat tertinggi pada limit fungsi di atas! Pangkat tertinggi pada pembilang adalah 2 (x²), pangkat tertinggi pada penyebut juga sama dengan 2.

Karena pembilang dan penyebut mempunyai pangkat tertinggi sama, nila limitnya merupakan koefisien dari pangkat tertinggi tersebut.

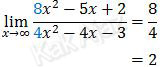
Jadi, nilai limit mendekati tak hingga tersebut adalah 2 (C).

Soal No. 24 tentang Turunan Fungsi Aljabar

Pembahasan

Turunan pertama dari fungsi aljabar dirumuskan sebagai:

y = xⁿ
y’ = nx^n-1

Mari kita turunkan fungsi aljabar di atas. Setelah itu kita substitusikan x = 1.

  f(x) = x³ − 9x + 5
f ‘(x) = 3x² − 9
f ‘(1) = 3×1² − 9
         = 3 − 9
         = −6

Jadi, nilai f ‘(1) dari fungsi tersebut adalah −6 (B).

Soal No. 25 tentang Aplikasi Turunan

Pembahasan

Grafik suatu fungsi dikatakan naik apabila turunan pertama fungsi tersebut bernilai positif.

f(x) = 2x³ − 3x² − 72x − 9

Grafik fungsi f(x) naik bila:

              f ‘(x) > 0
6x² − 6x − 72 > 0
    x² − x − 12 > 0
(x − 4)(x + 3) > 0

Pembuat nol pertidaksamaan tersebut adalah:

x = 4 dan x = −3

Selanjutnya kita buat garis bilangan untuk pertidaksamaan di atas.

Karena tanda pertidaksamaannya ‘>’ interval daerah pertidaksamaannya berada di sebelah kiri −3 atau sebelah kanan 4.

Jadi, grafik fungsi f(x) naik pada interval x < −3 atau x > 4 (A).

Simak Pembahasan Soal Matematika IPS UN 2017 selengkapnya.

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih