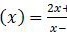pembahasan selanjutnya adalah
- invers fungsi,
- sistem pertidaksamaan linear,
- model matematika program linear,
- penyelesaian program linear, dan
- kesamaan matriks.
Soal No. 11 tentang Invers Fungsi
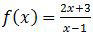
untuk x ≠ 1 dan f−1 adalah invers dari f. Nilai dari f−1(−3) adalah ….
A. −6
B. −6/5
C. 0
D. 6/5
E. 6
Pembahasan
Invers fungsi bentuk pecahan linear di atas dapat diselesaikan dengan rumus:

Berdasarkan rumus di atas, diperoleh:
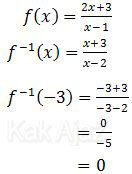
Jadi, nilai dari f−1(−3) adalah 0 (C).
Soal No. 12 tentang Sistem Pertidaksamaan Linear
A. 144
B. 124
C. 39
D. 27
E. 19

Pembahasan
Gambar daerah sistem pertidaksamaan di atas adalah sebagai berikut:
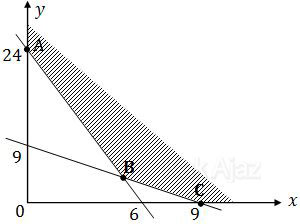
Nilai minimum yang mungkin pada sistem pertidaksamaan di atas berada di titik A, B, atau C.
Sekarang perhatikan fungsi objektifnya!
f(x, y) = 3x + 6y
Koefisien x pada fungsi objektif di atas jauh lebih kecil dari koefisien y. Sehingga dapat dipastikan nilai minimumnya berada di sumbu x, yaitu titik C(9, 0).
f(9, 0) = 3×9 + 6×0
= 27
Jadi, nilai minimum fungsi objektif pada sistem pertidaksamaan tersebut adalah 27 (D).
Soal No. 13 tentang Model Matematika Program Linear
A. 3x + 4y ≥ 8; x + 2y ≥ 5; x ≥ 0; y ≥ 0
B. 3x + 4y ≥ 8; 2x + 4y ≥ 5; x ≥ 0; y ≥ 0
C. 4x + 3y ≥ 8; 2x + y ≥ 5; x ≥ 0; y ≥ 0
D. 4x + 3y ≥ 8; x + y ≥ 5; x ≥ 0; y ≥ 0
E. 4x + 2y ≥ 8; 3x + y ≥ 5; x ≥ 0; y ≥ 0
Pembahasan
Untuk mempermudah menentukan model matematikanya, kita buat tabel bantuan sebagai berikut:
| Tablet (x) | Kapsul (y) | ||
| Kalsium | 3 |
4 |
8 |
| Vitamin A | 1 |
2 |
5 |
Keterangan: angka yang dicoret tersebut artinya dibagi 50.
Berdasarkan tabel di atas, diperoleh:
3x + 4y ≥ 8
x + 2y ≥ 5
Jadi, model matematika sistem pertidaksamaan tersebut adalah opsi (A).
Soal No. 14 tentang Penyelesaian Program Linear
A. Rp75.000,00
B. Rp100.000,00
C. Rp115.000,00
D. Rp125.000,00
E. Rp160.000,00
Pembahasan
Misal:
x : kado jenis A
y : kado jenis B
Tabel bantuan untuk soal di atas adalah:
| Kado A (x) | Kado B (y) | ||
| Kertas | 1 |
1 |
25 |
| Pita | 2 | 1 | 40 |
| Upah | 5.000 | 4.000 | ? |
Berdasarkan tabel bantuan di atas diperoleh:
x + y = 25
2x + y = 40
⎯⎯⎯⎯⎯⎯⎯ − (bawah dikurangi atas)
x = 15
Substitusi x = 15 ke persamaan yang pertama diperoleh:
x + y = 25
15 + y = 25
y = 15
Dengan demikian, upah pembungkusan kado adalah:
Upah = 5.000x + 4.000y
= 5.000×15 + 4.000×10
= 75.000 + 40.000
= 115.000
Jadi, upah maksimum yang dapat diterima oleh karyawati tersebut adalah Rp115.000,00 (C).
Soal No. 15 tentang Kesamaan Matriks
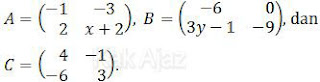
Jika 2A − B = CT dengan CT adalah transpos dari matriks C, nilai x + y = ….
A. −5
B. −3
C. −1
D. 1
E. 5
Pembahasan
Transpos suatu matriks adalah komponen baris matriks tersebut yang diposisikan sebagai komponen kolom.
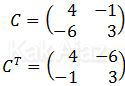
Nah, sekarang kita masuk ke kesamaan matriks.
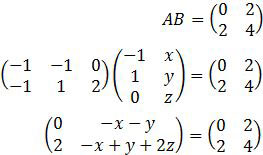
Perhatikan komponen kanan bawah!
2x + 13 = 3
2x = −10
x = −5
Sekarang perhatikan kiri bawah!
−3y + 5 = −1
−3y = −6
y = 2
Dengan demikian, nilai x + y adalah:
x + y = −5 + 2
= −3
Jadi, nilai dari x + y adalah −3 (B).
Simak Pembahasan Soal Matematika IPS UN 2016 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat