Pembahasan Matematika IPA UN: Sudut antara Dua Vektor

Pembahasan soal-soal Ujian Nasional (UN) SMA-IPA bidang studi Matematika dengan materi pembahasan Sudut antara Dua Vektor yang meliputi:

• besar sudut antara dua vektor, 
• nilai sinus atau kosinus sudut antara dua vektor.

Soal tentang Sudut antara Dua Vektor UN 2012

Pembahasan

Langkah pertama kita tentukan komponen vektor AB dan vektor AC.

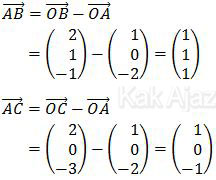
Selanjutnya kita gunakan rumus sudut antara dua vektor.

Jadi, sudut antara vektor AB dengan vektor AC adalah 90° (D).

Soal tentang Sudut antara Dua Vektor UN 2010

Pembahasan

Untuk menentukan sudut antara vektor u dan v kita perlu menghitung perkalian kedua vektor tersebut dan panjang masing-masing vektor.

u ∙ v = 1∙1 + √2∙(−√2) + √5∙√5
        = 1 − 2 + 5
        = 4

|u| = √[1² + (√2)² + (√5)²]
    = √8

|v| = √[1² + (−√2)² + (√5)²]
    = √8

Sudut antara vektor u dan v dirumuskan sebagai:

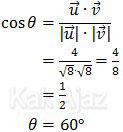
Jadi, Sudut antara vektor u dan v adalah 60° (C).

Soal tentang Sudut antara Dua Vektor UN 2013

Pembahasan

Kita tentukan dulu operasi vektor yang diperlukan.

p ∙ q = −2 − 1 + 0
        = −3

|p| = √[1² + 1² + (−4)²]
     = √18
     = 3√2

|q| = √[(−2)² + (−1)²]
     = √5

Sudut antara vektor p dan q dirumuskan sebagai:

Untuk mendapatkan nilai sinus sudut, kita gunakan rumus identitas trigonometri.

sin²⁡ θ = 1 − cos²⁡ θ
          = 1 − 1/10
          = 9/10
  sin⁡θ = ±3/(√10) 
          = ±3/10 √10 (kuadran II atau III)

Teks soal tidak menyebutkan interval sudut. Bila yang dimaksud kuadran II maka jawabannya +3/10 √10, sedangkan bila yang dimaksud kuadran III maka jawabannya adalah −3/10 √10.

Jadi, nilai sinus sudut antara vektor p dan q adalah ±3/10 √10 (A/E).

Soal tentang Sudut antara Dua Vektor UN 2015

Pembahasan

Panjang vektor a + b merupakan resultan dari penjumlahan vektor a dan b sehingga berlaku:

 |a + b|² = |a|² + |b|² + 2|a||b| cos⁡ θ
         8² = 4² + 6² + 2∙4∙6 cos ⁡θ
         64 = 52 + 48 cos⁡ θ
48 cos ⁡θ = 12
     cos ⁡θ = 1/4

Karena yang ditanyakan nilai dari cos⁡ 2θ maka kita gunakan rumus kosinus sudut ganda.

cos⁡ 2θ = 2 cos²⁡ θ − 1
           = 2 (1/4)² − 1
           = 1/8 − 1
           = −7/8

Jadi, nilai dari cos⁡ 2θ adalah −7/8 (A).

Soal tentang Sudut antara Dua Vektor UN 2014

Pembahasan

Proyeksi u pada v adalah p, ini berarti bahwa vektor v adalah searah dengan vektor p atau vektor v merupakan kelipatan dari vektor p.

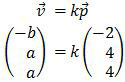
Dari kesamaan vektor di atas diperoleh:

−b = −2k
  k = 1/2 b

a = 4k
   = 4 ∙ 1/2 b
   = 2b

Nah, sekarang kita substitusikan a = 2b pada komponen vektor u dan v.

u = ai + 9j + bk
   = 2bi + 9j + bk

v = −bi + aj + ak
   = −bi + 2bj + 2bk

Selanjutnya kita gunakan rumus sudut antara dua vektor. Namun, sebelumnya kita tentukan dulu operasi vektor yang diperlukan pada rumus tersebut.

u ∙ v = −2b² + 18b + 2b²
        = 18b

|u| = √[(2b)² + 9² + b²]
     = √(5b² + 81)

|v| = √[(−b)² + (2b)² + (2b)²]
    = √(9b²)
    = 3b

Kita masukkan data-data di atas pada rumus sudut antara dua vektor.

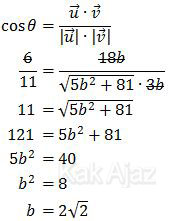
Jadi, nilai b adalah 2√2 (C).

Pembahasan soal lain tentang Sudut antara Dua Vektor bisa disimak di:
Pembahasan Matematika IPA UN 2013 No. 16
Pembahasan Matematika IPA UN 2014 No. 15
Pembahasan Matematika IPA UN 2015 No. 17

Simak juga:
Pembahasan Matematika IPA UN: Operasi Vektor
Pembahasan Matematika IPA UN: Proyeksi Vektor

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih