Pembahasan Matematika IPA UN: Integral Fungsi Aljabar

Pembahasan soal-soal Ujian Nasional (UN) SMA-IPA bidang studi Matematika dengan materi pembahasan Integral Fungsi Aljabar yang meliputi integral tentu dan tak tentu serta integral substitusi dan parsial.

Integral Tentu Fungsi Aljabar UN 2012

Pembahasan

Integral di atas adalah integral biasa. Tingkat kesulitannya hanya saat memasukkan batas.

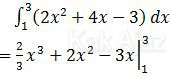
Langkah pengintegralan sudah selesai. Langkah selanjutnya adalah memasukkan batas.

Masukkan batas x = 1 dan x = 3 langsung per suku seperti di bawah ini:

= ⅔ (3³ − 1³ ) + 2(3² − 1² ) − 3(3 − 1)
= ⅔ ∙ 26 + 2 ∙ 8 − 3 ∙ 2
= (52)/3 + 16 − 6
= 17⅓ + 10
= 27⅓

Jadi, hasil dari integral tersebut adalah 27⅓ (A).

Integral Tentu Fungsi Aljabar UN 2013

Pembahasan

Fungsi yang diintegral kita kalikan dulu.

   3(x + 1)(x − 6)
= 3(x² − 5x − 6)
= 3x² − 15x − 18

Dengan demikian, integral di atas menjadi:

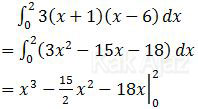
Batas x = 0 tidak perlu kita masukkan karena pasti akan menghasilkan nol. Dengan memasukkan x = 2 diperoleh:

= 2³ − (15)/2 ∙ 2² − 18 ∙ 2
= 8 − 30 − 36
= −58

Jadi, hasil dari integral tersebut adalah −58 (A).

Integral Tentu Fungsi Aljabar UN 2015

Hasil

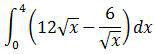
adalah ….

A.   88
B.   80
C.   64
D.   40
E.   24

Pembahasan

Bentuk akar pada soal di atas kita ubah dulu menjadi bentuk pangkat.

Bentuk terakhir ini masih terkesan sulit. Sebaiknya dilakukan pengubahan sebagai berikut:

x^1/2 = √x
x^3/2 = x^1½
       = x√x

Dengan demikian, bentuk tersebut menjadi:

= 8x√x − 12√x |⁴
= 8 ∙ 4√4 − 12√4
= 8 ∙ 8 − 12 ∙ 2
= 64 − 24
= 40

Jadi, hasil dari integral tersebut adalah 40 (D).

Integral Substitusi Fungsi Aljabar UN 2014

Hasil

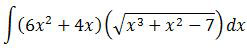
adalah ….

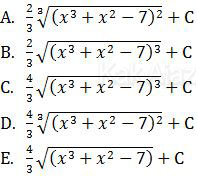
Pembahasan

Integral di atas adalah integral substitusi. Cirinya, pangkat x di luar dan di dalam akar mempunyai selisih 1.

Langkah pertama adalah mengubah bentuk akar menjadi bentuk pangkat.

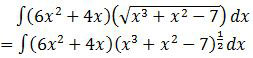
Selanjutnya kita lakukan pengubahan terhadap dx.

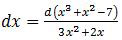
dx diganti dengan d(x³ + x² − 7) karena mempunyai pangkat x lebih tinggi. Sedangkan 3x² + 2x adalah turunan dari x³ + x² − 7.

Dengan demikian, integral di atas menjadi:

Perhatikan, 6x² + 4x dapat dicoret dengan 3x² + 2x menghasilkan 2 sehingga integral tersebut bisa langsung diselesaikan.

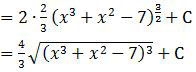
Jadi, hasil dari integral substitusi tersebut adalah opsi (C).

Integral Parsial Fungsi Aljabar UN 2005

Hasil dari

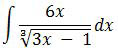
adalah ….

Pembahasan

Integral di atas adalah integral parsial. Cirinya, pangkat x di luar dan di dalam akar adalah sama.

Penyelesaian integral parsial yang paling praktis adalah metode Tanzalin.

Pertama, kita pisahkan menjadi dua fungsi. Fungsi yang sederhana kita turunkan sedangkan fungsi yang lebih rumit kita integralkan.

Perhatikan bagan metode Tanzalin berikut!

Hasil dari integral tersebut adalah perkalian miring sebagaimana yang ditunjukkan oleh garis biru.

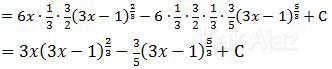
Jadi, hasil dari integral parsial tersebut adalah opsi (E).

Pembahasan soal Integral Fungsi Aljabar yang lain bisa disimak di:
Pembahasan Matematika IPA UN 2013 No. 31 dan 33
Pembahasan Metamatika IPA UN 2014 No. 30
Pembahasan Metamatika IPA UN 2014 No. 31
Pembahasan Metamatika IPA UN 2015 No. 32 dan 33
Pembahasan Metamatika IPA UN 2016 No. 31 dan 32
Pembahasan Matematika IPA UN 2017 No. 23 dan 24
Pembahasan Matematika IPA UN 2018 No. 20
Pembahasan Matematika IPA UN 2018 No. 21
Pembahasan Matematika IPA UN 2019 No. 20
Pembahasan Matematika IPA UN 2019 N0. 21
Pembahasan Matematika IPA UN 2019 (2) No. 20
Pembahasan Matematika IPA UN 2019 (2) No. 21

Simak juga, Pembahasan Matematika IPA UN: Integral Fungsi Trigonometri.

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih