Pembahasan Matematika IPA UN 2019 No. 6

Pembahasan soal-soal Ujian Nasional (UN) tahun 2019 bidang studi Matematika SMA-IPA nomor 6 sampai dengan nomor 10 tentang:

• fungsi, 
• komposisi fungsi, 
• invers fungsi,
• matriks, dan 
• transformasi geometri.

Soal No. 6 tentang Fungsi

Agar fungsi

terdefinisi maka daerah asal f(x) adalah ….

A.   {x│x ≤ −4/3, x ≠ −2, x ∈ R}
B.   {x│x ≥ 4/3, x ∈ R}
C.   {x│x ≥ −2, x ∈ R}
D.   {x│−2 ≤ x ≤ 4/3, x ∈ R}
E.   {x│x ≤ −2 atau x ≥ 4/3, x ∈ R}

Pembahasan

Fungsi di atas adalah fungsi akar. Agar terdefinisi, fungsi tersebut harus memenuhi syarat akar: yang diakar harus lebih besar atau sama dengan nol.

Sementara itu, fungsi yang diakar berbentuk pecahan sehingga penyebutnya tidak boleh sama dengan nol.

x + 2 ≠ 0
     x  ≠ −2

Garis bilangan dari kedua syarat tersebut adalah:

Dengan demikian hasil penyelesaiannya adalah:

x ≥ 4/3

Jadi, daerah asal fungsi tersebut adalah opsi (B).

Perdalam materi ini di Soal FUNGSI Matematika UN SMA-IPA dan Pembahasan.

Soal No. 7 tentang Komposisi Fungsi

Pembahasan

Diketahui:

(f ∘ g)(x) = f(g(x)) = x³ − 6x² + 10x − 3
Ditanyakan f(2)

Berarti:

 g(x) = 2
x − 2 = 2
      x = 4

Dengan demikian, nilai f(2) diperoleh saat x = 4.

f(g(x)) = x³ − 6x² + 10x − 3
    f(2) = 4³ − 6 . 4² + 10 . 4 − 3
           = 64 − 96 + 40 − 3
           = 5

Jadi, nilai dari f(2) adalah 5 (D).

Perdalam materi ini di Pembahasan Matematika UN: Komposisi dan Invers Fungsi.

Soal No. 8 tentang Invers Fungsi

Pembahasan

Menentukan invers fungsi atau fungsi kebalikan dapat dilakukan dengan cara meletakkan variabel x di ruas kiri terlebih dahulu.

f(x) = √(2x + 3)
    y = √(2x + 3)
  y² = 2x + 3
  2x = y² − 3
    x = 1/2 (y² − 3)

Kemudian x di ruas ini kita ubah menjadi f^-1(x) sedangkan y di ruas kanan kita ubah menjadi x.

f^-1(x) = 1/2 1/2 (x² − 3)

Nah, sekarang tinggal memasukkan nilai x = 3.

f^-1(3) = 1/2 (3² − 3)
          = 1/2 ⋅ 6
          = 3

Jadi, nilai dari f^-1(3) adalah 3 (B).

Perdalam materi ini di Pembahasan Matematika UN: Komposisi dan Invers Fungsi.

Soal No. 9 tentang Matriks

Diketahui

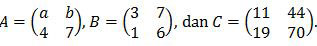
Jika AB = C maka nilai a + b = ….

A.   2
B.   5
C.   6
D.   7
E.   10

Pembahasan

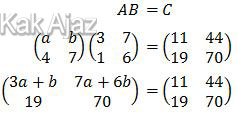
Diperoleh persamaan linear:

3a + b = 11
7a + 6b = 44

Mari kita eliminasikan kedua persamaan tersebut dengan mengalikan 6 pada persamaan kedua

18a + 6b = 66 (dikalikan 6)
  7a + 6b = 44
⎯⎯⎯⎯⎯⎯⎯⎯⎯  −
        11a = 22
            a = 2

Substitusi a = 2 ke persamaan pertama diperoleh:

3 ⋅ 2 + b = 11
            b = 5

Dengan demikian,

a + b = 2 + 5
         = 7

Jadi, nilai a + b adalah 7 (D).

Perdalam materi ini di Pembahasan Matematika UN: Matriks.

Soal No. 10 tentang Transformasi Geometri

Pembahasan

Matriks transformasi X berordo 2×2, misal

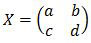
Bayangan A oleh transformasi X berlaku hubungan

Sehingga diperoleh:

b = 2
d = 3

Demikian juga bayangan B oleh transformasi X berlaku hubungan

Sehingga diperoleh:

a + 2b = 5
c + 2d = 7

Substitusi b = 2 dan d = 3 pada kedua persamaan di atas diperoleh:

a + 2∙2 = 5
          a = 1

c + 2∙3 = 7
         c = 1

Dengan demikian matriks transformasi X adalah:

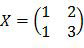
Sedangkan invers matriks transformasi X adalah:

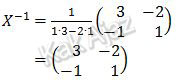
Untuk menentukan titik C dari C’ berlaku hubungan:

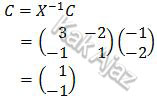
Jadi, titik C adalah (1,-1) (A).

Perdalam materi ini di Pembahasan Matematika UN: Transformasi Geometri.

Simak Pembahasan Soal Matematika IPA UN 2019 selengkapnya.

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih