pembahasan selanjutnya adalah

Pembahasan soal-soal Ujian Nasional (UN) tahun 2019 bidang studi Matematika SMA-IPA nomor 37 sampai dengan nomor 40 tentang:
- barisan dan deret,
- aturan sinus dan kosinus,
- kaidah pencacahan, dan
- aplikasi turunan.
SOAL ISIAN
Soal No. 37 tentang Barisan dan Deret
- Setiap tim terdiri dari 5 orang dan setiap anggota kelompok harus mengambil kelereng sesuai urutannya.
- Pada pengambilan putaran pertama (5 orang secara bergantian) hanya diperbolehkan mengambil masing-masing satu kelereng.
- Pada putaran ke-n (n ≥ 2), orang pertama setiap kelompok mengambil n kelereng dan selalu bertambah 3 kelereng untuk peserta pada urutan berikutnya dalam kelompok tersebut.
Tim C beranggotakan Aldo, Bambang, Candra, Didi, dan Eka (urutan pengambilan kelereng sesuai dengan urutan abjad awal nama). Bersamaan habisnya waktu, ternyata Candra adalah anggota Tim C terakhir yang berhasil mengambil 11 kelereng. Banyak kelereng yang berhasil dikumpulkan oleh Tim C adalah … kelereng.
Pembahasan
Akan lebih praktis bila soal di atas dibahas dengan tabel berikut ini.
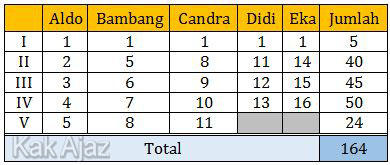
Jadi, banyak kelereng yang berhasil dikumpulkan oleh Tim C adalah 164 kelereng.
Soal No. 38 tentang Aturan dan Sinus dan Kosinus
Sebuah kapal berlayar dari pelabuhan P pada pukul 07.00 WIB dengan arah jurusan tiga angka 050° dan sampai di pelabuhan Q pada pukul 13.00 WIB. Pukul 14.00 WIB kapal bergerak kembali dari pelabuhan Q ke pelabuhan R dengan arah jurusan tiga angka 170° dan sampai di pelabuhan R pada pukul 18.00 WIB. Kecepatan rata-rata kapal 40 mil/jam. Jika p adalah jarak pelabuhan P ke pelabuhan R dalam mil, nilai p2 adalah ….
Pembahasan
Jarak antara pelabuhan P dan Q adalah:
s = vt
= 40 mil/jam × 6 jam
= 240 mil
Jarak antara pelabuhan Q dan R adalah:
s = vt
= 40 mil/jam × 4 jam
= 160 mil
Sekarang perhatikan rute perjalanan kapal berikut ini!

Jarak dicari dengan aturan kosinus segitiga. Pandang segitiga PQR!
PR2 = PQ2 + QR2 − 2 ∙ PQ ∙ QR ∙ cos Q
p2 = 2402 + 1602 − 2 ∙ 240 ∙ 160 ∙cos 60°
= 57600 + 25600 − 2 ∙ 240 ∙ 160 ∙ 1/2
= 44800
Jadi, nilai p2 adalah 44.800.
Perdalam materi ini di Pembahasan Matematika UN: Aturan Sinus dan Kosinus.
Soal No. 39 tentang Kaidah Pencacahan
Zaki akan membuat sebuah alamat email. Untuk keperluan itu, ia memerlukan sebuah kata sandi (password) yang terdiri dari delapan karakter. Kata sandi dikatakan baik jika menggabungkan antara huruf dan angka. Zaki akan menggunakan namanya pada empat karakter awal atau akhir secara berturut-turut, kemudian ditambahkan dengan empat buah angka dari 0, 1, 2, …, 9 secara acak, misalnya ZAKI1234, ZAKI0021, 4321ZAKI, 3334ZAKI, dan lain-lain. Banyaknya kata sandi email yang dapat digunakan adalah ….
Pembahasan
Kata “ZAKI” selalu tetap urutannya sehingga yang perlu dihitung adalah 4 angka sebelum atau sesudah kata ‘ZAKI’.
Empat tersebut disusun dari 10 angka yang boleh berulang sehingga banyak susunan yang mungkin adalah:
10 × 10 × 10 × 10 = 10.000
Dengan demikian, jumlah kata sandi adalah:
Nama ZAKI di awal = 10.000 kata sandi
Nama ZAKI di akhir = 10.000 kata sandi
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
Total = 20.000 kata sandi
Jadi, banyaknya kata sandi email yang dapat digunakan adalah 20.000 kata.
Perdalam materi ini di Pembahasan Matematika UN: Kaidah Pencacahan.
Soal No. 40 tentang Aplikasi Turunan
Sebuah akuarium berbentuk balok tanpa tutup memiliki alas berbentuk persegi panjang dengan perbandingan lebar dan panjangnya 2 : 3. Jika luas permukaan akuarium adalah 1.800 cm2, volume maksimum akuarium tersebut adalah ….
Pembahasan
Perbandingan lebar dan panjangnya 2 : 3. Misal:
panjang : 3x
lebar : 2x
tinggi : t
Luas permukaan akuarium tanpa tutup dirumuskan:
L = pl + 2pt + 2lt
1800 = 3x ∙ 2x + 2 ∙ 3x ∙ t + 2 ∙ 2x ∙ t
1800 = 6x2 + 6xt + 4xt
10xt = 1800 − 6x2
t = 180/x − 0,6x
Volume akuarium tersebut dirumuskan:
V = plt
= 3x ∙ 2x ∙ t
= 6x2t
= 6x2 (180/x − 0,6x)
= 1080x − 3,6x3
Agar volume mencapai maksimum, turunan V harus sama dengan nol.
V’ = 0
1080 − 10,8x2 = 0
10,8x2 = 1080
x2 = 100
x = 10
Dengan demikian, volume akuarium mencapai maksimum saat nilai x = 10. Mari kita masukkan nilai x tersebut pada persamaan volume.
V = 1080x − 3,6x3
= 1080 × 10 − 3,6 × 103
= 10800 − 3600
= 7200
Jadi, volume maksimum akuarium tersebut adalah 7.200 cm3.
Perdalam materi ini di Pembahasan Matematika UN: Aplikasi Turunan.
Simak Pembahasan Soal Matematika IPA UN 2019 selengkapnya.
Simak juga:
Pembahasan Matematika IPA UN 2013
Pembahasan Matematika IPA UN 2014
Pembahasan Matematika IPA UN 2015
Pembahasan Matematika IPA UN 2016
Pembahasan Matematika IPA UN 2017
Pembahasan Matematika IPA UN 2018
Pembahasan Matematika IPA UN 2019 Paket 2
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
