pembahasan selanjutnya adalah

Pembahasan soal Ujian Nasional (UN) tahun 2019 bidang studi Matematika SMA-IPA Paket 2 nomor 31 sampai dengan nomor 36 tentang:
- statistika [ukuran pemusatan],
- kaidah pencacahan [kejadian saling bebas],
- teori peluang [kejadian saling bebas],
- teori peluang [frekuensi harapan], dan
- teori peluang [kejadian saling asing].
Soal No. 31 tentang Statistika [ukuran pemusatan]
Pembahasan
Rata-rata data di atas adalah:
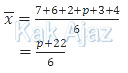
Sedangkan median (Me) adalah nilai tengah setelah data diurutkan. Karena banyaknya data ada 6, mediannya terletak di antara data ke-3 dan ke-4.
Rata-rata dan median untuk bilangan asli p = 1, 2, 3
1, 2, 3, 4, 6, 7
2, 2, 3, 4, 6, 7
2, 3, 3, 4, 6, 7
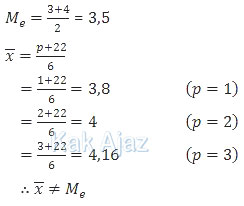
Rata-rata dan median untuk bilangan asli p = 4
2, 3, 4, 4, 6, 7
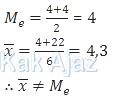
Rata-rata dan median untuk bilangan asli p = 5
2, 3, 4, 5, 6, 7
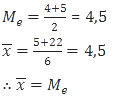
Rata-rata dan median untuk bilangan asli p = 6
2, 3, 4, 6, 6, 7
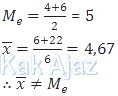
Rata-rata dan median untuk bilangan asli p = 7
2, 3, 4, 6, 7, 7
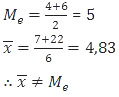
Rata-rata dan median untuk bilangan asli p = 8
2, 3, 4, 6, 7, 8
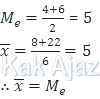
Untuk bilangan asli p lebih dari 8, median tetap 5 sedangkan rata-rata di atas 5. Sehingga rata-rata data tersebut selalu tidak sama dengan nilai mediannya.
Dengan demikian, hanya ada 2 nilai p yang membuat data tersebut mempunyai rata-rata dan median yang sama, yaitu 5 dan 8.
Jadi, banyaknya nilai p bilangan asli adalah 2 (A).
Perdalam materi ini di Pembahasan Matematika UN: Statistika.
Soal No. 32 tentang Kaidah Pencacahan [kejadian saling bebas]
| A. | 7 cara |
| B. | 9 cara |
| C. | 12 cara |
| D. | 18 cara |
| E. | 21 cara |
Pembahasan
Banyak cara memilih 2 larutan dari 4 larutan P adalah:
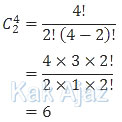
Banyak cara memilih 1 larutan dari 3 larutan Q adalah:
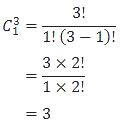
Banyak cara memilih 2 larutan P dan 1 larutan Q adalah:
Jadi, banyak cara memilih 2 larutan P dan 1 larutan Q ada 18 cara (D).
Perdalam materi ini di Pembahasan Matematika UN: Kaidah Pencacahan.
Soal No. 33 tentang Kaidah Pencacahan [kejadian saling bebas]
| A. | 560 cara |
| B. | 1.120 cara |
| C. | 1.560 cara |
| D. | 1.680 cara |
| E. | 2.240 cara |

Pembahasan
Dari 12 orang akan dipilih 3 pemain inti dan 1 pemain pengganti untuk setiap regu (ada 3 regu). Sudah ditetapkan 3 orang sebagai tekong (anggap saja pemain inti 1) sehingga tersisa 9 orang.
Dari 9 orang tersebut kemudian ditetapkan 3 orang lagi sebagai pemain inti 2.
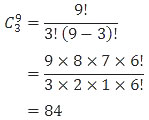
Tersisa 6 orang yang belum terpilih. Dari 6 orang ini kemudian ditetapkan 3 orang lagi sebagai pemain inti 3.
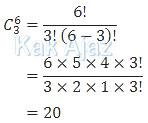
Tersisa 3 orang. 3 orang ini sudah pasti akan menempati pemain pengganti. Untuk memastikan, Kak Ajaz hitung saja, meski hasilnya sudah pasti 1. Hitung-hitung supaya pembahasannya lebih panjang.
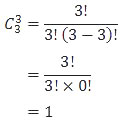
Dengan demikian, banyak menempatkan pemain lain (pemain inti 2, pemain inti 3, dan pemain pengganti adalah:
| 9C3 × 6C3 × 3C3 | = | 84 × 20 × 1 |
| = | 1680 |
Jadi, banyak cara menempatkan pemain lain ke dalam regu adalah 1.680 cara (D).
Perdalam materi ini di Pembahasan Matematika UN: Kaidah Pencacahan.
Soal No. 34 tentang Teori Peluang [kejadian saling bebas]
| A. | 1/132 |
| B. | 1/72 |
| C. | 1/66 |
| D. | 1/36 |
| E. | 1/6 |
Pembahasan
Dalam sebuah kardus terdapat 12 telepon genggam, 10 di antaranya dalam kondisi baik dan 2 rusak. Peluang terambilnya telepon yang rusak adalah:
2/12 = 1/6
Sekarang di dalam kardus terdapat 11 telepon, 1 rusak dan 10 baik. Peluang terambilnya telepon rusak dalam kardus tersebut adalah:
1/11
Dengan demikian, peluang terambilnya 2 telepon rusak pada 2 pengambilan pertama adalah
1/6 × 1/11 = 1/66
Jadi, peluang diperoleh 2 telepon genggam rusak pada dua pengujian yang pertama adalah 1/66 (C).
Perdalam materi ini di Pembahasan Matematika UN: Teori Peluang.
Soal No. 35 tentang Teori Peluang [frekuensi harapan]
| A. | 14 kali |
| B. | 21 kali |
| C. | 28 kali |
| D. | 35 kali |
| E. | 42 kali |
Pembahasan
Diketahui:
| S | = | 1 ,2, 3, 4, 5, 6, 7, 8, 9, 10 |
| n(S) | = | 10 |
| A | = | bola dengan nomor bilangan prima |
| = | 2, 3, 5, 7 | |
| n(A) | = | 4 |
| N | = | 70 |
Peluang muncul bola dengan nomor bilangan prima adalah:
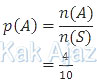
Frekuensi harapan muncul bola dengan nomor bilangan prima adalah:
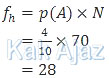
Jadi, frekuensi harapan muncul bola dengan nomor bilangan prima adalah 28 kali (C).
Perdalam materi ini di Pembahasan Matematika UN: Teori Peluang.
Soal No. 36 tentang Teori Peluang [kejadian saling asing]
| A. | 5/6 |
| B. | 2/3 |
| C. | 1/2 |
| D. | 2/9 |
| E. | 4/15 |
Pembahasan
Ada 4 kemungkinan agar minimal 2 siswa mencapai KKM.
Andi gagal, Tito dan Vian lolos
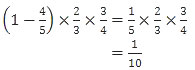
Tito gagal, Andi dan Van lolos
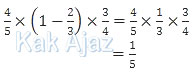
Vian gagal, Andi dan Tito lolos
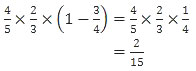
Ketiganya lolos
Dengan demikian, peluang minimal 2 siswa mencapai KKM adalah:
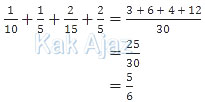
Jadi, peluang bahwa minimal dua di antara tiga siswa tersebut dapat mencapai nilai KKM adalah 5/6 (A).
Perdalam materi ini di Pembahasan Matematika UN: Teori Peluang.
Simak Pembahasan Soal Matematika IPA UN 2019 Paket 2 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
