pembahasan selanjutnya adalah

Pembahasan soal Ujian Nasional (UN) tahun 2019 bidang studi Matematika SMA-IPA Paket 2 nomor 21 sampai dengan nomor 25 tentang:
- integral substitusi,
- trigonometri,
- grafik fungsi trigonometri,
- aturan sinus dan kosinus, serta
- dimensi tiga [jarak titik ke garis].
Soal No. 21 tentang Integral Substitusi
| A. | ⅓ (x2 − x + 3)3 + C |
| B. | ¼ (x2 − x + 3)3 + C |
| C. | ¼ (x2 − x + 3)4 + C |
| D. | ½ (x2 − x + 3)4 + C |
| E. | (x2 − x + 3)4 + C |
Pembahasan
Integral di atas termasuk integral substitusi. Cirinya, terdiri dari dua fungsi dengan derajat (pangkat tertinggi) berselisih satu.
Adapun cara penyelesaiannya sebagai berikut:
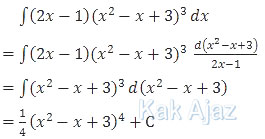
Jadi, hasil dari integral tersebut adalah (C).
Perdalam materi ini di Pembahasan Matematika UN: Integral Fungsi Aljabar.
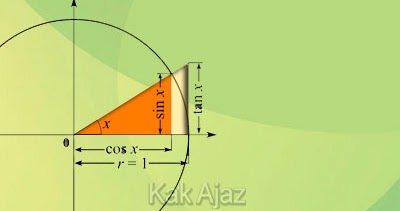
Soal No. 22 tentang Trigonometri

Pembahasan
Perhatikan gambar berikut ini!

Karena α sudut lancip (kuadran I) maka semua nilai trigonometri bernilai positif.

Jadi, nilai dari cscα adalah opsi (D).
Perdalam materi ini di Pembahasan Matematika UN: Perbandingan Trigonometri.
Soal No. 23 tentang Grafik Fungsi Trigonometri

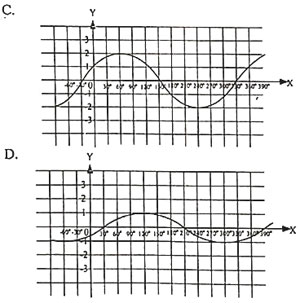
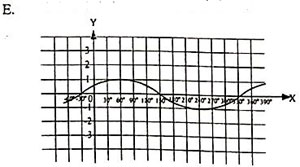

Pembahasan
Fungsi f(x) = 2 sin (x − 30)° sudah tampak jelas mempunyai amplitudo 2. [opsi C, D, dan E salah]
Sekarang kita tentukan pembuat nol-nya.
| y | = | |
| 2 sin (x − 30)° | = | |
| sin (x − 30)° | = | |
| x − 30° | = | 0°, 180°, 360°, … |
| x | = | 30°, 210°, 390°, … |
Grafik fungsi sinus dengan pembuat nol di atas adalah:
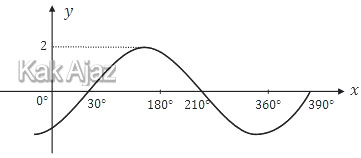
Jadi, grafik fungsi f(x) = 2 sin (x − 30)° adalah grafik pada opsi (A).
Perdalam materi ini di Fungsi Trigonometri dan Grafknya [Soal UN dan Pembahasan].
Soal No. 24 tentang Aturan Sinus dan Kosinus
| A. | 50√6 m |
| B. | 100√3 m |
| C. | 150√2 m |
| D. | 100√6 m |
| E. | 300√6 m |
Pembahasan
Perhatikan gambar berikut ini!

Karena diketahui dua sudut dan satu sisi, kita gunakan aturan sinus segitiga.

Jadi, jarak antara tonggak A dan C adalah 100√6 m (D).
Perdalam materi ini di Pembahasan Matematika UN: Aturan Sinus dan Kosinus.
Soal No. 25 tentang Dimensi Tiga [jarak titik ke garis]
| A. | 3√7 cm |
| B. | 3√6 cm |
| C. | 3√5 cm |
| D. | 3√3 cm |
| E. | 2√3 cm |
Pembahasan
Perhatikan gambar berikut ini!
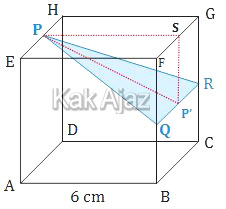
Jarak titik P ke garis QR, yaitu PP’ merupakan tinggi segitiga PQR. Selain itu, PP’ juga merupakan sisi miring segitiga siku-siku PP’S. Sehingga,

Jadi, jarak dari titik P ke garis QR adalah 3√5 cm (C).
Perdalam materi ini di Pembahasan Matematika UN: Dimensi Tiga.
Simak Pembahasan Soal Matematika IPA UN 2019 Paket 2 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat