pembahasan selanjutnya adalah

Pembahasan soal-soal Ujian Nasional (UN) tahun 2018 bidang studi Matematika SMA-IPA nomor 6 sampai dengan nomor 10 tentang:
- sistem persamaan linear [umur],
- sistem persamaan linear [bangun datar],
- sistem pertidaksamaan linear,
- program linear, dan
- matriks.
Soal No. 6 tentang Sistem Persamaan Linear [umur]
A. 52 tahun
B. 54 tahun
C. 56 tahun
D. 62 tahun
E. 64 tahun
Pembahasan
Misal:
x : umur ibu
y : umur anak
Pada tahun 2016, umur seorang ibu tiga kali umur anaknya. Anggap saja sekarang tahun 2016.
x = 3y … (1)
Pada tahun 2010 umur ibu lima kali umur anaknya. Berarti 6 tahun yang lalu (masing-masing variabel dikurangi 6).
x − 6 = 5(y − 6)
x − 6 = 5y − 30
x = 5y − 24 … (2)
Kita substitusikan persamaan (1) ke persamaan (2).
3y = 5y − 24
24 = 2y
y = 12
Dengan demikian umur anak pada tahun 2016 adalah 12 tahun, sedangkan umur ibu adalah:
x = 3y
= 3 × 12 tahun
= 36 tahun
Sehingga pada tahun 2020 (4 tahun yang akan datang):
Umur ibu : 36 + 4 = 40
Umur anak : 12 + 4 = 16
Jumlah : 40 + 16 = 56
Jadi, jumlah umur mereka pada tahun 2020 adalah 56 tahun (C).
Perdalam materi ini di Pembahasan Matematika UN: Sistem Persamaan Linear
Soal No. 7 tentang Sistem Persamaan Linear [bangun datar]
A. 48 cm2
B. 44 cm2
C. 28 cm2
D. 14 cm2
E. 8 cm2

Pembahasan
Keliling sebuah persegi panjang 28 cm.
K = 28
2(p + l) = 28
p + l = 14 … (1)
Panjang persegi panjang tersebut 2 cm lebih panjang dari lebarnya.
p = l + 2 … (2)
Substitusi persamaan (2) ke persamaan (1) diperoleh:
p + l = 14
l + 2 + l = 14
2l + 2 = 14
2l = 12
l = 6
Sehingga lebar persegi panjang adalah 6 cm, sedangkan panjangnya adalah:
p = l + 2
= 6 + 2
= 8
Dengan demikian luasnya adalah:
L = p × l
= 8 × 6
= 48
Jadi, luas dari persegi panjang tersebut adalah 48 cm2 (A).
Perdalam materi ini di Pembahasan Matematika UN: Sistem Persamaan Linear
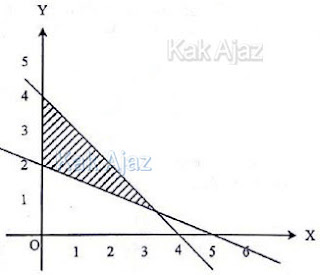
Soal No. 8 tentang Sistem Pertidaksamaan Linear
A. x + y ≤ 4, 2x + 5y ≥ 10, y ≥ 0
B. x + y ≤ 4, 2x + 5y ≤ 10, y ≥ 0
C. x + y ≤ 4, 2x + 5y ≥ 10, x ≥ 0
D. x + y ≥ 4, 2x + 5y ≥ 10, x ≥ 0
E. x + y ≥ 4, 2x + 5y ≤ 10, x ≥ 0
Pembahasan
Sebelum menjawab soal di atas, Kak Ajaz ingatkan kembali konsep berikut ini!
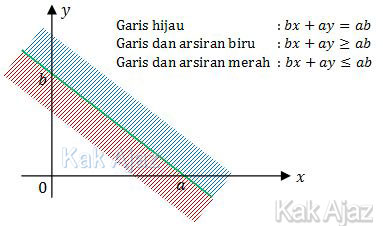
Nah, mari kita selesaikan berdasarkan konsep di atas!
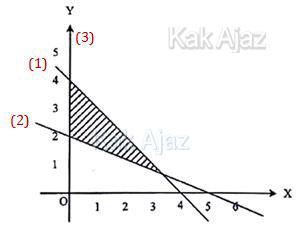
Daerah arsiran pada grafik di atas dibatasi oleh garis (1), garis (2), dan garis (3).
Garis (1) dan daerah arsiran di bawahnya:
4x + 4y ≤ 16
x + y ≤ 4
Garis (2) dan daerah arsiran di atasnya:
2x + 5y ≥ 10
Garis (3) atau garis x = 0 (sumbu y) dan daerah di sebelah kanannya:
x ≥ 0
Jadi, daerah himpunan penyelesaian semua (x, y) yang memenuhi sistem pertidaksamaan opsi (C).
Perdalam materi ini di Sistem Pertidaksamaan Linear [Soal UN dan Pembahasan].
Soal No. 9 tentang Program Linear
A. Rp500.000,00
B. Rp540.000,00
C. Rp600.000,00
D. Rp700.000,00
E. Rp720.000,00
Pembahasan
Untuk mempermudah, Kak Ajaz buat tabel bantu sebagai berikut:

Berdasarkan tabel bantuan di atas diperoleh:
- x + y = 20 … (1)
- x + 3y = 30 … (2)
- fungsi objektif z = 30.000x + 50.000y
Eliminasi persamaan (1) dan (2)
x + y = 20
x + 3y = 30
⎯⎯⎯⎯⎯⎯⎯ − [bawah dikurangi atas]
2y = 10
y = 5
Substitusi y = 5 ke persamaan (1)
x + y = 20
x + 5 = 20
x = 15
Selanjutnya, nilai x dan y tersebut kita substitusikan ke fungsi objektif.
z = 30.000x + 50.000y
= 30.000 × 15 + 50.000 × 5
= 450.000 + 250.000
= 700.000
Jadi, pendapatan maksimum dari hasil penjualan kedua jenis minuman tersebut adalah Rp700.000,00 (D).
Perdalam materi ini di Pembahasan Matematika IPA UN: Program Linear
Soal No. 10 tentang Matriks

Jika matriks C = AB, invers matriks C adalah C−1 = ….

Pembahasan
Langkah pertama kita kalikan matriks A dan B untuk mendapatkan matriks C.

Selanjutnya kita tentukan invers matriks C dengan menggunakan rumus:
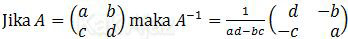
Berdasarkan rumus di atas, invers matriks C adalah:

Jadi, invers matriks C adalah opsi (B).
Perdalam materi ini di Pembahasan Matematika IPA UN: Matriks
Simak Pembahasan Soal Matematika IPA UN 2018 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat