pembahasan selanjutnya adalah
Pembahasan soal-soal Ujian Nasional (UN) tahun 2018 bidang studi Matematika SMA-IPA nomor 31 sampai dengan nomor 36 tentang:
- statistika [kuartil bawah],
- statistika [modus],
- kaidah pencacahan [susunan angka],
- kaidah pencacahan [susunan buku],
- kaidah pencacahan [kombinasi], dan
- peluang kejadian.
Soal No. 31 tentang Statistika [kuartil bawah]
| Interval | Frekuensi |
| 40 – 44 | 12 |
| 45 – 49 | 20 |
| 50 – 54 | 15 |
| 55 – 59 | 30 |
| 60 – 64 | 12 |
| 65 – 69 | 11 |
A. 44,50
B. 45,75
C. 46,50
D. 46,75
E. 47,75
Pembahasan
Jumlah data pada tabel di atas adalah:
N = 100
Kelas kuartil bawah (Q1) terletak pada 1/4 data pertama.
¼ N = ¼ × 100
= 25
Berarti kelas kuartil pada terletak pada baris kedua.
Perhatikan tabel berikut beserta besaran-besaran yang diperlukan dalam menentukan nilai kuartil bawah.
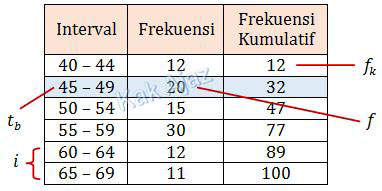
Berdasarkan tabel di atas diperoleh data:
tb = 45 − 0,5
= 44,5
i = 65 − 60
= 5
fk = 12
f = 20
Dengan demikian, nilai kuartil bawah data di atas adalah:

Jadi, kuartil bawah dari data pada tabel distribusi frekuensi di atas adalah 47,25 47,75 (E).
Perdalam materi ini di Pembahasan Matematika IPA UN: Statistika
Soal No. 32 tentang Statistika [modus]

Nilai tes siswa terbanyak adalah ….
A. 74,75
B. 75,50
C. 75,75
D. 76,50
E. 77,50

Pembahasan
Nilai siswa terbanyak adalah nilai modus. Nilai modus berada pada kelas dengan frekuensi tertinggi, yaitu terletak pada 74,5 – 79,5.
Untuk menentukan nilai modus, perhatikan analisis histogram berikut ini!

Berdasarkan analisis histogram di atas diperoleh:
tb = 74,5
d1 = 15 − 9 = 6
d1 = 15 − 6 = 9
i = 89,5 − 84,5 = 5
Nilai modus dapat ditentukan dengan rumus:

Jadi, nilai tes siswa terbanyak adalah 76,50 (D).
Perdalam materi ini di Pembahasan Matematika IPA UN: Statistika
Soal No. 33 tentang Kaidah Pencacahan [susunan angka]
A. 120
B. 80
C. 64
D. 60
E. 40
Pembahasan
Cara 1 (perkalian)
Dari angka-angka 2, 3, 5, 6, 8, 9 (6 angka) disusun bilangan 3 angka. Bilangan 3 angka adalah bilangan ratusan.
Agar nilainya lebih dari 500 maka angka yang menempati posisi ratusan haruslah 5, 6, 8, dan 9 (4 angka). Posisi puluhan dan satuan boleh diisi angka berapa saja.
Jumlah angka yang menempati posisi puluhan hanya 5 angka karena 1 angka telah menempati posisi ratusan. Sedangkan jumlah angka yang menempati posisi satuan hanya 4 angka karena 2 angka masing-masing menempati posisi puluhan dan ratusan.

Hasilnya adalah:
4 × 5 × 5 = 80
Cara 2 (permutasi)
Dari 6 angka disusun bilangan 3 angka.

Agar nilainya lebih dari 500 maka angka depan harus 5, 6, 8, dan 9 (4 angka dari 6 angka). Diperoleh:
4/6×120=80
Jadi, banyak bilangan lebih besar dari 500 yang bisa dibuat adalah 80 bilangan (B).
Perdalam materi ini di Pembahasan Matematika IPA UN: Kaidah Pencacahan
Soal No. 34 tentang Kaidah Pencacahan [susunan buku]
A. 1.728
B. 1.608
C. 864
D. 72
E. 36
Pembahasan
Banyak cara penyusunan daripada dirinci sebagai berikut:
- 3 rak masing-masing diisi pelajaran yang sama.
3! = 3 × 2 × 1
= 6
- Rak matematika terdiri dari 3 buku berbeda
3! = 6
- Rak fisika terdiri dari 2 buku yang sama
1! = 1
- Rak biologi terdiri 4 buku berbeda
4! = 4 × 3 × 2 × 1
= 24
Dengan demikian, banyaknya susunan yang mungkin adalah:
6 × 6 × 1 × 24 = 864
Jadi, Banyak cara menyusun buku-buku tersebut adalah 864 cara (C).
Perdalam materi ini di Pembahasan Matematika IPA UN: Kaidah Pencacahan
Soal No. 35 tentang Kaidah pencacahan [kombinasi]
A. 12
B. 19
C. 34
D. 60
E. 120
Pembahasan
Banyak cara memanggil 1 pria (dari 4 pria) dan 2 wanita (dari 6 wanita):
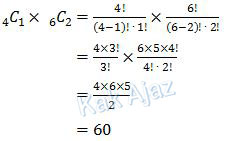
Jadi, banyaknya cara memanggil 1 pria dan 2 wanita adalah 60 cara (D).
Perdalam materi ini di Pembahasan Matematika IPA UN: Kaidah Pencacahan
Soal No. 36 tentang Peluang Kejadian
| Hari | Banyak komplek yang mengalami pemadaman |
| Senin | 4 |
| Selasa | 5 |
| Rabu | 3 |
| Kamis | 5 |
| Jumat | 4 |
| Sabtu | 5 |
| Minggu | 4 |
Jika jadwal pemadaman tersebut berlaku secara acak pada semua komplek, peluang terjadi pemadaman listrik di sebuah komplek pada hari Rabu atau Minggu adalah ….
A. 1/300
B. 1/10
C. 1/15
D. 13/100
E. 7/30
Pembahasan
Banyak seluruh komplek yang mengalami pemadaman listrik:
n(S) = 30
Misal A adalah kejadian pemadaman listrik pada hari Rabu dan B adalah pemadaman pada hari Minggu, maka:
n(A) = 3
n(B) = 4
Peluang kejadian A atau B adalah:

Jadi, peluang terjadi pemadaman listrik di sebuah komplek pada hari Rabu atau Minggu adalah 7/30 (E).
Perdalam materi ini di Pembahasan Matematika IPA UN: Teori Peluang
Simak Pembahasan Soal Matematika IPA UN 2018 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat