Pembahasan Matematika IPA UN 2018 No. 26

Pembahasan soal-soal Ujian Nasional (UN) tahun 2018 bidang studi Matematika SMA-IPA nomor 26 sampai dengan nomor 30 tentang:

• dimensi tiga [sudut antargaris], 
• persamaan lingkaran, 
• garis singgung lingkaran, 
• transformasi geometri, dan 
• statistika [kurva ogive].

Soal No. 26 tentang Dimensi Tiga [sudut antargaris]

Pembahasan

Perhatikan bangun kubus ABCD.EFGH berikut!

Garis EG dan garis CF tidak bertemu, untuk itu garis CF Kak Ajaz proyeksikan ke garis ED.

Pandang segitiga DEG!
DE adalah diagonal sisi. Demikian juga DG dan EG. Sehingga segitiga DEG adalah segitiga sama sisi.

Sama sisi berarti sama sudut. Tiap sudut segitiga sama sisi besarnya sama, yaitu:

180° ∶ 3 = 60°

Jadi, sudut antara garis EG dan garis CF adalah 60° (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Sudut antara Garis dan Bidang [Dimensi Tiga]

Soal No. 27 tentang Persamaan Lingkaran

Pembahasan

Persamaan lingkaran yang berpusat di P(3, 2) adalah:

(x − 3)² + (y − 2)² = r²

Persamaan lingkaran tersebut melalui titik Q(7, 5). Kita substitusikan titik Q untuk mendapatkan jari-jari r.

(7 − 3)² + (5 − 2)² = r²
                  4² + 3² = r²
                   16 + 9 = r²
                          r² = 25

Nah, sekarang kita kembali ke persamaan lingkaran dengan substitusi r² = 25.

(x − 3)² + (y − 2)² = r²
x² − 6x + 9 + y² − 4y + 4 = 25
x² + y² − 6x − 4y + 13 − 25 = 0
x² + y² − 6x − 4y − 12 = 0

Jadi, persamaan lingkaran yang berpusat di P(3, 2) dan melalui titik Q(7, 5) adalah opsi (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Lingkaran

Soal No. 28 tentang Garis Singgung Lingkaran

Pembahasan

Bentuk umum lingkaran x² + y² − 6x + 4y + 4 = 0 adalah:

x² + y² + Ax + By + C = 0

Dari bentuk umum tersebut diperoleh:

A = −6
B = 4
C = 4

Sehingga diperoleh:

Pusat lingkaran : (h, k) = (−½A, −½B)
                                     = (3, −2)

Jari-jari : r = √[¼ (A² + B²) − C]
                  = √[¼ (36 + 16) − 4]
                  = √9
                  = 3

Selanjutnya kita tentukan gradien. Gradien garis 5x + 12y − 12 = 0 adalah:

m₁ = −a/b
      = −5/12

Karena garis tersebut tegak dengan garis singgung lingkaran maka gradien garis singgung lingkaran adalah:

     m₁ ∙ m₂ = −1
−5/12 ∙ m₂ = −1
             m₂ = 12/5

Dengan demikian, persamaan garis singgung lingkaran adalah:

      y − k = m₂ (x − h) ± r √(m₂² + 1)
      y + 2 = 12/5 (x − 3) ± 3√(144/25 + 1)
      y + 2 = 12/5 (x − 3) ± 3 ∙ 13/5
  5y + 10 = 12(x − 3) ± 39       [dikalikan 5]
  5y + 10 = 12x − 36 ± 39
12x − 5y = 46 ∓ 39

Persamaan terakhir ini bisa kita uraian menjadi dua:

I.   12x − 5y = 46 − 39
      12x − 5y = 7

II.  12x − 5y = 46 + 39
      12x − 5y = 85

Jadi, persamaan garis singgung pada lingkaran tersebut adalah opsi (A).

Perdalam materi ini di Pembahasan Matematika IPA UN: Lingkaran

Soal No. 29 tentang Transformasi Geometri

Pembahasan

Matriks rotasi 180° adalah:

Bayangan titik oleh rotasi 180° dengan pusat rotasi (2, 2) adalah:

Dengan demikian,

(4, 3) → (−4 + 4, −3 + 4)
          → (0, 1)

(−1, 2) → (1 + 4, −2 + 4)
            → (5, 2)

(3, 5) → (−3 + 4, −5 + 4)
          → (1, −1)

Jadi, bayangan ketiga titik tersebut berturut-turut adalah opsi (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Transformasi Geometri

Soal No. 30 tentang Statistika [grafik ogive]

Perhatikan histogram berikut!

Grafik ogive positif yang sesuai dengan diagram tersebut adalah …

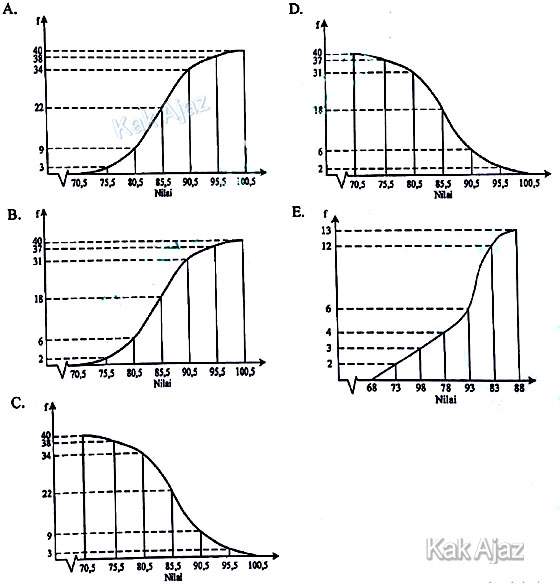
Pembahasan

Grafik ogive adalah grafik yang dibuat berdasarkan tabel distribusi kumulatif, baik kurang dari maupun lebih dari.

Grafik ogive positif dibuat berdasarkan frekuensi kumulatif kurang dari dengan batas tepi atas.

Jadi, grafik ogive positif yang sesuai dengan diagram tersebut adalah opsi (B).

Simak Pembahasan Soal Matematika IPA UN 2018 selengkapnya.

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih