pembahasan selanjutnya adalah

Pembahasan soal-soal Ujian Nasional (UN) tahun 2018 bidang studi Matematika SMA-IPA nomor 16 sampai dengan nomor 20 tentang:
- turunan fungsi,
- aplikasi turunan [fungsi naik],
- aplikasi turunan [garis singgung],
- aplikasi turunan [nilai minimum], dan
- integral tak tentu.
Soal No. 16 tentang Turunan Fungsi
A. 40x − 15
B. −20x2 + 24x − 9
C. 20x3 − 27x2 + 9x
D. 20x2 + 25x − 15
E. 60x2 − 54x + 9
Pembahasan
Kita turunkan dulu fungsi f(x) dan g(x).
f(x) = 5x − 3
f’(x) = 5
g(x) = 4x2 − 3x
g’(x) = 8x − 3
Fungsi h(x) terdiri dari fungsi f(x) dan g(x) sebagaimana fungsi y dan turunannya berikut ini.
y = u ∙ v
y’ = u’v + uv’
Dengan demikian turunan dari h(x) adalah:
h(x) = f(x) ∙ g(x)
h’(x) = f;(x) ∙ g(x) + f(x) ∙ g‘(x)
= 5(4x2 − 3x) + (5x − 3)(8x − 3)
= 20x2 − 15x + 40x2 − 15x − 24x + 9
= 60x2 − 54x + 9
Jadi, turunan dari fungsi h(x) adalah opsi (E).
Perdalam materi ini di Pembahasan Matematika IPA UN: Turunan Fungsi
Soal No. 17 tentang Aplikasi Turunan [fungsi naik]
A. −7/3 < x < 5
B. −3/7 < x < 5
C. −5 < x < 3/7
D. x < −5 atau x > 3/7
E. x < −3/7 atau x > 5

Pembahasan
Diketahui fungsi f(x) = 7/3 x3 + 16x2 − 15x + 6.
Fungsi f(x) dikatakan naik apabila turunan pertamanya positif.
f’(x) > 0
7x2 + 32x − 15 > 0
(7x − 3)(x + 5) > 0
Pembuat nol pertidaksamaan tersebut adalah:
x = 3/7 atau x = −5
Karena tanda pertidaksamaannya “>” maka intervalnya berada di sebelah kiri dan kanan pembuat nol.
x < −5 atau x > 3/7
Jadi, fungsi f(x) naik pada interval x < −5 atau x > 3/7 (D).
Perdalam materi ini di Pembahasan Matematika IPA UN: Titik Stasioner dan Nilai Ekstrem
Soal No. 18 tentang Aplikasi Turunan [garis singgung]
A. 3x − y + 4 = 0
B. 3x − y − 4 = 0
C. 3x − y − 20 = 0
D. x − 3y − 4 = 0
E. x − 3y + 4 = 0
Pembahasan
Gradien garis singgung kurva y = x2 − 5x + 12 adalah turunan pertama dari kurva tersebut.
m1 = y’
= 2x − 5
Sedangkan gradien garis 3x − y + 5 = 0 adalah:
m2 = −a/b
= −3/(−1)
= 3
Karena garis singgung kurva dan garis tersebut sejajar maka kedua gradien bernilai sama.
m1 = m2
2x − 5 = 3
2x = 8
x = 4
Nah, x = 4 ini merupakan absis titik singgung. Sekarang kita cari ordinatnya dengan cara substitusi absis tersebut pada persamaan kurva.
y = x2 − 5x + 12
= 42 − 5 ∙ 4 + 12
= 16 − 20 + 12
= 8
Sehingga titik singgungnya adalah:
(4, 8)
Persamaan garis singgungnya adalah:
y − y1 = m1(x − x1)
y − 8 = 3(x − 4)
y − 8 = 3x − 12
y − 3x + 4 = 0
Hasil ini ternyata tidak ada pada opsi jawaban. Coba masing-masing kita kalikan negatif.
−y + 3x − 4 = 0
3x − y − 4 = 0
Jadi, persamaan garis singgung kurva tersebut adalah opsi (B).
Perdalam materi ini di Pembahasan Matematika IPA UN: Titik Stasioner dan Nilai Ekstrem
Soal No. 19 tentang Aplikasi Turunan [nilai minimum]
A. Rp75.000.000,00
B. Rp80.000.000,00
C. Rp90.000.000,00
D. Rp120.000.000,00
E. Rp145.000.000,00
Pembahasan
Biaya produksi:
B = (4x + 100/x + 40) juta rupiah
Agar biaya produksi minimum maka:
B’ = 0
4 − 100/x2 = 0
4 = 100/x2
4x2 = 100
x2 = 25
x = ±5
Kita pakai x = 5 karena x menyatakan jumlah hari.
Dengan demikian, biaya produksi minimum terjadi saat x = 5.
B = (4x + 100/x + 40) juta rupiah
= (4∙5 + 100/5 + 40) juta rupiah
= (20 + 20 + 40) juta rupiah
= 80 juta rupiah
Jadi, biaya minimum produksi industri rumah tangga tersebut adalah Rp80.000.000,00 (B).
Perdalam materi ini di Pembahasan Matematika IPA UN: Titik Stasioner dan Nilai Ekstrem
Soal No. 20 tentang Integral Tak Tentu

Pembahasan
Bentuk integral di atas adalah integral substitusi. Cirinya, terdiri dari dua fungsi serta pangkat tertinggi dari dua fungsi tersebut berselisih 1.
Mari kita selesaikan bersama-sama!

Sampai di sini, dx kita ganti dengan d(x2 − 2x + 10) kemudian dibagi dengan x2 − 2x + 10.

Yang tercetak merah kita coret dan menghasilkan 1/2.
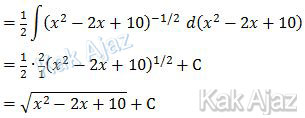
Jadi, hasil dari integral substitusi tersebut adalah opsi (D).
Perdalam materi ini di Pembahasan Matematka IPA UN: Integral Fungsi Aljabar
Simak Pembahasan Soal Matematika IPA UN 2018 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
