Pembahasan Matematika IPA UN 2018 No. 11

Pembahasan soal-soal Ujian Nasional (UN) tahun 2018 bidang studi Matematika SMA-IPA nomor 11 sampai dengan nomor 15 tentang:

• matriks, 
• barisan dan deret aritmetika, 
• barisan dan deret geometri, 
• aplikasi barisan aritmetika, serta 
• limit fungsi.

Soal No. 11 tentang Matriks

Banyaknya siswa laki-laki di sebuah kelas adalah 2/5 siswa perempuan. Jika 12 orang siswa perempuan meninggalkan kelas itu maka banyaknya siswa perempuan dan laki-laki menjadi sama. Jika x dan y berturut-turut menyatakan banyaknya siswa laki-laki dan perempuan maka matriks yang tepat untuk menyatakan banyaknya masing-masing siswa adalah ….

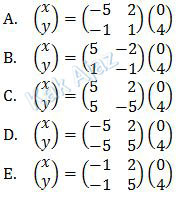
Pembahasan

Banyaknya siswa laki-laki di sebuah kelas adalah 2/5 siswa perempuan.

          x = 2/5 y
        5x = 2y
5x − 2y = 0      … (1)

Jika 12 orang siswa perempuan meninggalkan kelas itu maka banyaknya siswa perempuan dan laki-laki menjadi sama.

y − 12 = x
  y − x = 12
  x − y = −12    … (2)

Mari kita sandingkan persamaan (1) dan (2) menjadi sistem persamaan.

5x − 2y = 0
    x − y = −12

Bentuk matriks untuk sistem persamaan di atas adalah:

Sekarang tinggal kita selesaikan (ingat rumus invers matriks pada pembahasan nomor 10).

Jadi, matriks yang tepat untuk menyatakan banyaknya masing-masing siswa adalah opsi (E).

Perdalam materi ini di Pembahasan Matematika IPA UN: Matriks

Soal No. 12 tentang Barisan dan Deret Aritmetika

Pembahasan

Kita tentukan dulu beda barisan aritmetika di atas dengan memanfaatkan rumus:

U_n = a + (n − 1)b

U₇ = a + 6b = 34
U₃ = a + 2b = 14
       ⎯⎯⎯⎯⎯⎯⎯⎯  −
               4b = 20
                 b = 5

Selanjutnya kita tentukan suku awal dengan memanfaatkan data U₃.

a = U₃ − 2b
   = 14 − 2 ∙ 5
   = 4

Nah sekarang kita gunakan rumus jumlah n suku pertama untuk menyelesaikan soal di atas.

 S_n = ½ n[2a + (n − 1)b]
S₂₃ = ½ ∙ 23(2 ∙ 4 + 22 ∙ 5)
      = ½ ∙ 23(8 + 110)
      = ½ ∙ 23 ∙118
      = 1357

Jadi, jumlah 23 suku pertama dari barisan tersebut adalah 1357 (B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Barisan dan Deret

Soal No. 13 tentang Barisan dan Deret Geometri

Pembahasan

Perhatikan deret geometri berikut!

−54 + 36 − 24 + ⋯

Dari deret geometri di atas dapat diperoleh data:

• suku awal : a = −54
• rasio         : r = 36/(−54) = −2/3

Suku ke-7 dapat dicari dengan rumus:

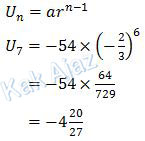
Jadi, suku ke-7 dari deret geometri tersebut adalah opsi (B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Barisan dan Deret

Soal No. 14 tentang Aplikasi Barisan Geometri

Pembahasan

Misal label A, B, C, D, dan berturut-turut adalah U₁, U₂, U₃, U₄, dan U₅ maka:

U₂ = 12
U₅ = 96
S₅ = ?

Rasio barisan geometri tersebut adalah:

Suku pertama deret tersebut bisa dicari dari suku ke-2 atau suku ke-5. Kak Ajaz gunakan suku ke-2 saja supaya lebih sederhana.

a = U₂/r
   = 12/2
   = 6

Jumlah 5 suku pertama barisan geometri tersebut dapat ditentukan dengan rumus:

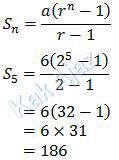
Jadi, jumlah seluruh kelereng yang diisikan ke dalam 5 kotak tersebut adalah 186 butir (B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Barisan dan Deret

Soal No. 15 tentang Limit Fungsi

Nilai dari

A.   3
B.   1
C.   −1
D.   −2
E.   −3

Pembahasan

Limit fungsi di atas adalah limit dalam bentuk:

Sekarang kita ubah limit pada soal di atas.

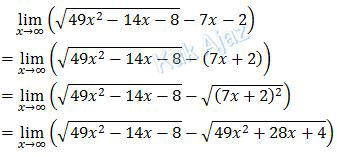
Sehingga diperoleh:

a = 49
b = −14
d = 28

Hasil akhir limit di atas dirumuskan:

Jadi, nilai dari limit tersebut adalah -3 (E).

Perdalam materi ini di Pembahasan Matematika IPA UN: Limit Fungsi

Simak Pembahasan Soal Matematika IPA UN 2018 selengkapnya.

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih