Pembahasan Matematika IPA UN 2015 No. 36

• aplikasi integral untuk menentukan luas daerah, 
• aplikasi integral untuk menentukan volume benda putar, 
• statistika, 
• kaidah pencacahan, dan 
• teori peluang.

Soal No. 36 tentang Aplikasi Integral untuk Menentukan Luas Daerah

Pembahasan

Pembuat nol kurva tersebut terhadap sumbu x adalah 

y = 0 
x³ − x² − 6x = 0 
x(x² − x − 6) = 0 
x(x − 3)(x + 2) = 0 
x = 0, x = 3, dan x = −2

Berdasarkan pembuat nol, grafik kurva tersebut adalah

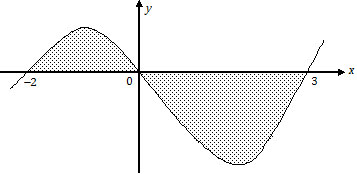
Daerah antara x = −2 sampai x = 0 berada di atas sumbu x sedangkan daerah antara x = 0 sampai x = 3 berada di bawah sumbu x. Dengan demikian, luas daerah yang dimaksud adalah

    
     = [¼(0−16) − ⅓(0+8) − 3(0−4)] − [¼(81−0) − ⅓(27−0) − 3(9−0)]
     = (−4 − 8/3 + 12) − (81/4 − 9 − 27)
     = 44 − 8/3 − 81/4
     = 44 − 275/12
     = 21 1/12

Jadi, luas daerah antara kurva dan sumbu x tersebut adalah opsi (E).

Perdalam materi ini di Pembahasan Matematika IPA UN: Luas Daerah [Aplikasi Integral].

Soal No. 37 tentang Aplikasi Integral untuk Menentukan Volume Benda Putar

Pembahasan

Pembuat nol kurva tersebut pada sumbu x adalah 

          y = 0
2x − x² = 0
x(2 − x) = 0 
x = 0 dan x = 2

Pembuat nol tersebut akan menjadi batas integrasi. Selanjutnya, mari kita tentukan volume benda putar tersebut.

Jadi, volume benda putar yang terjadi adalah opsi (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Volume Benda Putar [Aplikasi Integral].

Soal No. 38 tentang Statistika

Histogram berikut menunjukkan data umur penghuni rumah kontrakan milik Pak Achmad.

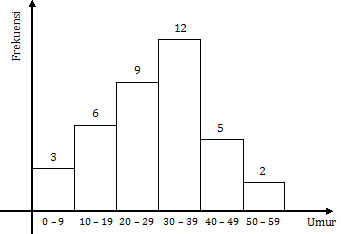
Modus data tersebut adalah ….

Artkel Terkait  Problem Teknologi Pendidikan Era Pandemi: Spektrum, Inovasi, dan Tantangan 

A.   29,5
B.   32,5
C.   33,5
D.   34,5
E.   35,5

Pembahasan

Perhatikan histogram di bawah ini!

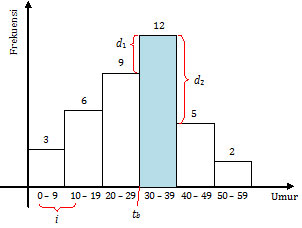
Daerah yang paling tinggi dan diarsir berwarna biru adalah kelas modus. Data yang berkaitan dengan kelas modus adalah 

i : lebar kelas 
i = 10 − 0
  = 10 

t_b : tepi bawah kelas modus
t_b = 30 − 0,5
    = 29,5 

d₁ : selisih frekuensi kelas modus dengan kelas sebelumnya. 
d₁ = 12 − 9
     = 3 

d₂ : selisih frekuensi kelas modus dengan kelas sesudahnya 
d₂ = 12 − 5
     = 7

Nah, sekarang kita tinggal memasukkan data-data tersebut pada rumus modus.

      
       = 32,5

Jadi, modus untuk data yang disajikan dalam histogram tersebut adalah 32,5 (B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Statistika. 

Soal No. 39 tentang Kaidah Pencacahan

Pembahasan

Karena ketua, sekretaris, dan bendahara kedudukannya bertingkat maka soal tersebut harus diselesaikan dengan permutasi.

         = 20 . 19 . 18
         = 6.840

Jadi, banyaknya susunan pengurus yang mungkin adalah 6.840 susunan (B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Kaidah Pencacahan, Permuatasi, dan Kombinasi.

Soal No. 40 tentang Teori Peluang

Pembahasan

Dalam 5 kali tendangan, penjaga gawang tersebut mampu menahan tendangan sebanyak 3 kali, dapat dinotasikan dengan kombinasi

3 kali tendangan dapat ditahan dengan peluang 3/5

(3/5)³ = 27/125

2 kali tendangan gagal ditahan dengan peluang 1 − 3/5 = 2/5

(2/5)² = 4/25

Dengan demikian, peluang penjaga gawang tersebut adalah 

     ₅C₃ . (3/5)³ . (2/5)²
= 10 . 27/125 . 4/25
= 216/625

Jadi, peluang penjaga gawang tersebut mampu menahan 3 kali tendangan penalti adalah 216/625 (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Teori Peluang.

Simak Pembahasan Soal Matematika IPA UN 2015 selengkapnya.

Simak juga,
Pembahasan Matematika IPA UN 2013
Pembahasan Matematika IPA UN 2014
Pembahasan Matematika IPA UN 2016
Pembahasan Matematika IPA UN 2017
Pembahasan Matematika IPA UN 2018
Pembahasan Matematika IPA UN 2019
Pembahasan Matematika IPA UN 2019 Paket 2

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih