Pembahasan Matematika IPA UN 2015 No. 21

• grafik fungsi logaritma, 
• barisan dan deret aritmetika, 
• deret geometri tak hingga, 
• dimensi tiga (jarak titik ke garis), serta 
• dimensi tiga (sudut antarbidang).

Soal No. 21 tentang Grafik Fungsi Logaritma

Pembahasan

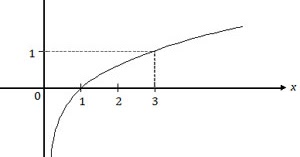
Berdasarkan grafik tersebut  diperoleh data:

Artinya, untuk x = 1 dihasilkan y = 0 dan untuk x = 3 dihasilkan y = 1.

Cara sederhana untuk mendapatkan nilai tersebut adalah trial and error, yaitu diujicobakan pada setiap opsi jawaban.

Opsi A:  y = ³log x
x = 1 → y = ³log 1 = 0 (benar) 
x = 3 → y = ³log 3 = 1 (benar)

Bisa dipastikan opsi yang lain salah.

Jadi, persamaan grafik fungsi tersebut adalah y = ³log x (A).

Soal No. 22 tentang Barisan dan Deret Aritmetika

Pembahasan

Barisan aritmetika dengan suku ke-3 = 2 dan suku ke-8 = −13. 

U₃ = a + 2b = 2         ….. (1) 
U₈ = a + 7b = −13     ….. (2)
       —————— −
             −5b = 15
                 b = −3

Substitusi b = −3 ke persamaan (1) untuk mendapatkan nilai a. 

a + 2b = 2 
  a − 6 = 2 
        a = 8

Jumlah 20 suku pertama.

S_n  = ½n[2a + (n − 1)b]
S₂₀ = 10[16 + 19.(−3)]
      = 10 . (−41)
      = −410

Jadi, jumlah 20 suku pertama deret tersebut adalah −410 (D).

Soal No. 23 tentang Deret Geometri Tak Hingga

Pembahasan

Perhatikan ilustrasi berikut ini!

Lintasan bola dalam kotak bergaris merah terdiri dari 2 jenis lintasan, yaitu lintasan naik dan lintasan turun . Kedua jenis lintasan tersebut panjangnya sama dan membentuk deret geometri tak hingga dengan suku awal t₂ dan rasio ⅔. 

a = t₂
   = ⅔ t₁
   = ⅔ × 9
   = 6

Dengan demikian, panjang seluruh lintasan (L) adalah panjang t₁ ditambah 2 kali jumlah deret tak hingga. 

L = t₁ + 2 S_∞
  
  
   = 9 + 36
   = 45

Jadi, panjang lintasan bola sampai berhenti adalah 45 meter (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Barisan dan Deret.

Soal No. 24 tentang Dimensi Tiga (Jarak Titik ke Garis)

Pembahasan

Perhatikan gambar kubus yang dimaksud berikut ini!

Panjang EM = MC.

        
         = 2√5

Panjang EC merupakan diagonal ruang.

EC = a√3
      = 4√3

QM adalah tinggi segitiga EMC dengan alas EC.

        
         = 2√2

Nah, mari kita perhatikan segitiga EMC dengan tinggi QM dan alas EC. Luas segitiga tersebut adalah 

L = ½ . EC . QM
   = ½ . 4√3 . 2√2
   = 4√6

Sekarang mari kita perhatikan lagi segitiga EMC. Kali ini dengan alas MC dan tinggi EP (yang ditanyakan). 

    L = ½ . MC . EP
4√6 = ½ . 2√5 . EP
  EP = 4√(6/5)
        = ⅘√30

Jadi, Jarak titik E ke garis CM adalah ⅘√30 cm (A).

Perdalam materi ini di Pembahasan Matematika IPA UN: Jarak Titik, Garis, dan Bidang [Dimensi Tiga].

Soal No. 25 tentang Dimensi Tiga (Sudut antarbidang)

Pembahasan

Perhatikan gambar kubus yang dimaksud berikut ini!

Bidang DEG dan BEG bertemu pada garis EG. Dari pertengahan garis EG ditarik garis ke B dan G sehingga terbentuk segitiga BDP. Sudut P pada segitiga BDP merupakan sudut yang dibentuk oleh bidang DEG dan BEG.

Panjang BP = DP.

       
        = 4√6

Panjang BD merupakan diagonal bidang.

BD = a√2
      = 8√2

Untuk menentukan sudut α, kita gunakan aturan kosinus segitiga. Perhatikan segitiga BDP.

Untuk mendapatkan nilai tan α dari cos α, kita gunakan perbandingan segitiga berikut ini.

Jadi, nilai tangen sudut antara bidang DEG dan BEG adalah 2√2 (E).

Perdalam materi ini di Pembahasan Matematika IPA UN: Sudut antara Garis dan Bidang [Dimensi Tiga].

Simak Pembahasan Soal Matematika IPA UN 2015 selengkapnya.

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih