Pembahasan Matematika IPA UN 2013 No. 36

Pembahasan soal-soal Ujian Nasional (UN) tahun 2013 bidang studi Matematika SMA-IPA nomor 36 sampai dengan nomor 40 tentang:

• statistika [kuartil bawah], 
• kaidah pencacahan, 
• kaidah pencacahan [aturan pengisian tempat], 
• kaidah pencacahan [aturan perkalian], dan 
• peluang kejadian.

Soal No. 36 tentang Statistika [Kuartil Bawah]

Pembahasan

Kuartil bawah atau Q₁ adalah nilai dari seperempat data pertama. Untuk itu, kita harus menentukan kelas kuartil bawah dulu.

    N = 40
¼ N = 10

Perhatikan tabel dan besaran-besaran kuartil bawah berikut ini!

Berdasarkan tabel di atas, diperoleh:

t_b = 155 − 0,5 = 154,5
i  = 175 − 170 = 5
f_k = 4
f  = 10

Kuartil bawah dapat ditentukan dengan rumus:

Jadi, kuartil bawah dari data pada tabel tersebut adalah 157,5 (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Statistika

Soal No. 37 tentang Kaidah Pencacahan

Pembahasan

Bilangan 3 angka adalah bilangan ratusan. Agar nilainya lebih dari 200 maka yang menempati posisi ratusan haruslah 2, 3, 5, 7, dan 9 (5 angka).

Sedangkan posisi puluhan bisa diisi angka berapa saja dari 6 angka yang disediakan, tetapi harus dikurangi 1 karena 1 angka tersebut sudah menempati posisi ratusan.

Posisi satuan juga bisa diisi angka berapa saja, tetapi harus dikurangi 2 karena 2 angka tersebut masing-masing sudah menempati puluhan dan ratusan.

Hasilnya adalah:

5 × (6 − 1) × (6 − 2) = 5 × 5 × 4
                                 = 100

Jadi, banyak bilangan 3 angka yang mungkin dapat disusun adalah 100 bilangan (A).

Perdalam materi ini di Pembahasan Matematika IPA UN: Kaidah Pencacahan

Soal No. 38 tentang Kaidah Pencacahan [Aturan Pengisian Tempat]

Pembahasan

Banyak cara 2 siswi selalu duduk paling pinggir:

2! = 2 × 1
    = 2

Banyak empat siswa duduk di antara 2 siswi:

4! = 4 × 3 × 2 × 1
    = 24

Dengan demikian, banyak cara mereka duduk adalah:

2! × 4! = 2 × 24
            = 48

Jadi, banyak cara mereka duduk adalah 48 cara (B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Kaidah Pencacahan

Soal No. 39 tentang Kaidah Pencacahan [Aturan Perkalian]

Erik suka sekali main skateboard. Dia mengunjungi sebuah toko bersama SKATERS untuk mengetahui beberapa model.

Di toko ini dia dapat membeli skateboard yang lengkap. Atau, ia juga dapat membeli sebuah papan, satu set roda yang terdiri dari 4 roda, satu set sumbu yang terdiri dari dua sumbu, dan satu set perlengkapan kecil untuk merakit skateboard sendiri.

Daftar barang dan model/jenis skateboard di toko ini sebagai berikut:

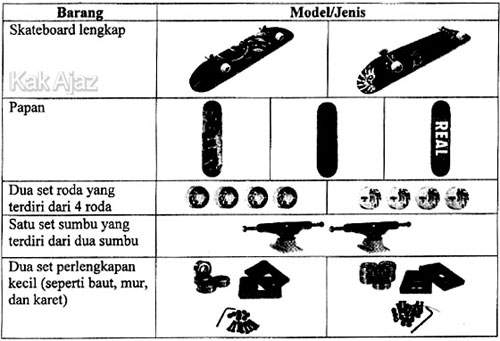
Toko itu menawarkan tiga macam papan, dua macam set roda, dan dua macam set perlengkapan kecil. Hanya ada satu macam set sumbu.

Berapa banyak skateboard yang dapat dibuat oleh Erik?

Artkel Terkait  Rangkuman, Contoh Soal & Pembahasan Fluida Statis

A.   6.
B.   8.
C.   10.
D.   12.
E.   24.

Pembahasan

Untuk merakit sebuah skateboard dibutuhkan sebuah papan, satu set roda, satu set sumbu, dan satu set perlengkapan kecil.

Sementara itu, di toko tersebut tersedia

• 3 macam papan
• 2 set roda
• 1 set sumbu
• 2 set perlengkapan kecil

Sehingga banyak skateboard yang dapat dibuat adalah:

3 × 2 × 1 × 2 = 12

Jadi, banyak skateboard yang dapat dibuat oleh Erik adalah 12 buah (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Kaidah Pencacahan

Soal No. 40 tentang Peluang Kejadian

Pembahasan

Jika A adalah terjadi gempa dalam 20 tahun ke depan maka Ac adalah tidak terjadi gempa dalam 20 tahun ke depan.

P(A) = 2/3
P(A^c) = 1 − 2/3
          = 1/3

Sehingga

P(A) > P(A^c)

Jadi, peluang terjadinya sebuah gempa bumi di kota Zadia pada suatu saat dalam 20 tahun ke depan lebih tinggi daripada peluang tidak terjadinya gempa bumi (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Teori Peluang

Simak Pembahasan Soal Matematika IPA UN 2013 selengkapnya.

Simak juga:
Pembahasan Matematika IPA UN 2014
Pembahasan Matematika IPA UN 2015
Pembahasan Matematika IPA UN 2016
Pembahasan Matematika IPA UN 2017
Pembahasan Matematika IPA UN 2018
Pembahasan Matematika IPA UN 2019
Pembahasan Matematika IPA UN 2019 Paket 2

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih