Pembahasan Matematika IPA UN 2013 No. 31

Pembahasan soal-soal Ujian Nasional (UN) tahun 2013 bidang studi Matematika SMA-IPA nomor 31 sampai dengan nomor 35 tentang:

• integral tentu fungsi aljabar, 
• integral tentu fungsi geometri, 
• integral tak tentu fungsi aljabar, 
• luas daerah [aplikasi integral], serta 
• volume benda putar [aplikasi integral].

Soal No. 31 tentang Integral Tentu Fungsi Aljabar

Hasil dari

A.   −58
B.   −56
C.   −28
D.   −16
E.   −14

Pembahasan

Kita operasikan dulu fungsi yang diintegralkan agar lebih mudah saat melakukan operasi integral nanti.

3(x + 1)(x − 6) = 3(x² − 5x − 6)
                        = 3x² − 15x − 18

Sehingga:

Cukup kita masukkan x = 2 saja karena x = 0 akan menghasilkan nol.

= 2³ − 15/2 ∙ 2² − 18 ∙ 2
= 8 − 30 − 36
= −58

Jadi, hasil integral fungsi aljabar di atas adalah −58 (A).

Perdalam materi ini di Pembahasan Matematika IPA UN: Integral Fungsi Aljabar

Soal No. 32 tentang Integral Tentu Fungsi Trigonometri

Nilai dari

A.   −1/3
B.   −1/2
C.   0
D.   1/3
E.   2/3

Pembahasan

Langkah pertama, kita pecah dulu sin³⁡x menjadi sin²⁡x ∙ sin⁡ x. Selanjutnya kita manfaatkan rumus sin²x + cos²⁡x = 1 untuk mengubah sin²⁡x.

Untuk batas integrasinya, Kak Ajaz lebih suka dalam bentuk derajat karena lebih familiar untuk orang Indonesia.

Ok, mari kita selesaikan!

Integral yang pertama adalah integral fungsi trigonometri biasa. Hasilnya adalah:

Sedangkan integral yang kedua adalah integral substitusi.

Dengan demikian,

Jadi, nilai dari integral fungsi trigonometri tersebut adalah 2/3 (E).

Perdalam materi ini di Pembahasan Matematika IPA UN: Intergral Fungsi Trigonometri

Soal No. 33 tentang Integral Tak Tentu Fungsi Aljabar

Hasil dari

Pembahasan

Kita kerjakan santai saja ya!

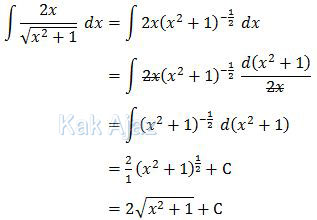
Jadi, hasil dari integral fungsi aljabar tersebut adalah opsi (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Integral Fungsi Aljabar

Soal No. 34 tentang Luas Daerah [Aplikasi Integral]

Luas daerah yang diarsir pada gambar dapat dinyatakan dengan rumus ….

Pembahasan

Daerah yang diarsir pada gambar di atas dibatasi oleh kurva y_k = x² dan garis y_g = x + 2.

Batas integrasinya merupakan titik potong antara kurva dan garis.

                  y_k = y_g
                  x² = x + 2
      x² − x − 2 = 0
(x + 1)(x − 2) = 0
x₁ = −1 dan x₂ = 2

Daerah yang diarsir berada di bawah garis dan di atas kurva (y_g berada di atas y_k) sehingga fungsi yang diintegral adalah:

y = y_g − y_k
   = x + 2 − x²

Dengan demikian, luas daerah yang diarsir adalah:

Jadi, rumus daerah yang diarsir adalah opsi (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Luas Daerah [Aplikasi Integral]

Soal No. 35 tentang Volume Benda Putar [Aplikasi Integral]

Pembahasan

Titik potong antara kurva dan garis tersebut adalah:

                 y_k = y_g
           x² + 1 = x + 3
     x² − x − 2 = 0
(x + 1)(x − 2) = 0
x₁ = −1 dan x₂ = 2

Kurva y = x² + 1 merupakan kurva parabola yang terbuka ke atas. Berarti garis y = x + 3 pasti berada di atas kurva (supaya terbentuk daerah). Lebih jelasnya perhatikan gambar berikut!

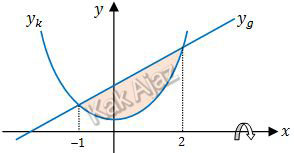
Volume benda putar yang terjadi adalah:

Sekarang tinggal kita masukkan batas integrasinya. Kak Ajaz lebih suka memasukkan kedua batas per suku. Maksudnya, setiap suku langsung Kak Ajaz masukkan dua batas.

Jadi, volume yang terjadi adalah 23 2/5 π satuan volume (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Volume Benda Putar [Aplikasi Integral]

Simak Pembahasan Soal Matematika IPA UN 2013 selengkapnya.

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih