Pembahasan Matematika IPA UN 2013 No. 21

Pembahasan soal-soal Ujian Nasional (UN) tahun 2013 bidang studi Matematika SMA-IPA nomor 21 sampai dengan nomor 25 tentang:

• barisan dan deret aritmetika, 
• barisan dan deret geometri, 
• dimensi tiga [jarak titik ke garis], 
• dimensi tiga [sudut antarbidang], serta 
• aturan sinus dan kosinus.

Soal No. 21 tentang Barisan dan Deret Aritmetika

Pembahasan

Suku ke-n barisan aritmetika dirumuskan:

U_n = a + (n − 1)b

Berdasarkan rumus di atas maka:

U₃ = a + 2b = 30
U₆ = a + 5b = 51
       ⎯⎯⎯⎯⎯⎯⎯⎯  −  [bawah dikurangi atas]
               3b = 21
                 b = 7

Selanjutnya b = 7 kita substitusikan ke U₃ untuk mendapatkan a.

   a + 2b = 30
a + 2 ∙ 7 = 30
   a + 14 = 30
           a = 16

Nah, sekarang kita sudah bisa menentukan S₁₅ melalui rumus:

S_n = n/2 [2a + (n − 1)b]
S₁₅ = 15/2 (2∙16 + 14∙7)
      = 15/2 (32 + 98)
      = 15/2 × 130
      = 975

Jadi, jumlah 15 suku pertama barisan tersebut adalah 975 (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Barisan dan Deret

Soal No. 22 tentang Barisan dan Deret Geometri

Pembahasan

Diketahui:

a = 200
U₄ = 1.600

Rasio barisan geometri tersebut adalah:

Jumlah 6 suku pertama adalah:

Jadi, Hasil produksi selama enam tahun adalah 12.600 unit (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Barisan dan Deret

Soal No. 23 tentang Dimensi Tiga [jarak titik ke garis]

Pembahasan

Perhatikan jarak yang dimaksud pada gambar berikut ini!

Segitiga AEG adalah segitiga siku-siku di E.

AE = rusuk kubus      = 6 cm
AG = diagonal ruang = 6√3 cm
EG = diagonal sisi     = 6√2 cm

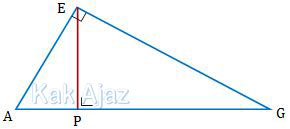
Jarak E ke AG adalah EP yang dirumuskan sumbu:

Jadi, jarak titik E ke garis AG adalah 2√6 cm (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Jarak Titik, Garis, dan Bidang

Soal No. 24 tentang Dimensi Tiga [sudut antarbidang]

Nilai kosinus sudut antara bidang BDE dan bidang BDG seperti terlihat pada gambar prisma segi-4 ABCD.EFGH beraturan berikut adalah ….

A.   2/6
B.   3/6
C.   4/6
D.   7/9
E.   8/9

Pembahasan

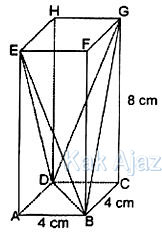
Perhatikan gambar berikut ini!

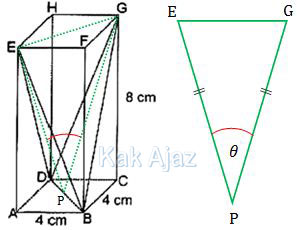
Segitiga EGP adalah segitiga sama kaki

EG = diagonal sisi = 4√2

EP = √(AE² + AP²), AP = 1/2 × diagonal sisi
      = √[8² + (2√2)²]
      = √(64 + 8)
      = √72
      = 6√2

Sudut θ bisa dicari dengan aturan kosinus segitiga sebagai berikut:

Jadi, nilai kosinus sudut antara bidang BDE dan bidang BDG adalah 7/9 (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Sudut antara Garis dan Bidang

Soal No. 25 tentang Aturan Sinus dan Kosinus

Pembahasan

Perhatikan gambar segi-12 berikut ini!

Pada segi-12 terdapat 12 segitiga sama kaki yang identik. Besar sudut tiap segitiga tersebut adalah:

θ = 360°/12
   = 30°

Panjang sisi segi-12 dapat ditentukan dengan aturan kosinus segitiga sebagai berikut:

s² = r² + r² − 2 ∙ r ∙ r ∙ cos 30°
    = 2r² − 2r² ∙ 1/2 √3
    = 2r² − r² √3
    = r² (2 − √3)
 s = r√(2 − √3)

Keliling segi-12 adalah 12 kali sisi tersebut.

K = 12s
    = 12r√(2 − √3)

Jadi, keliling segi-12 beraturan yang jari-jari lingkaran luarnya r cm adalah 12r√(2 − √3) cm (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Aturan Sinus dan Kosinus

Simak Pembahasan Soal Matematika IPA UN 2013 selengkapnya.

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih