Pembahasan Matematika IPA UN 2013 No. 16

Pembahasan soal-soal Ujian Nasional (UN) tahun 2013 bidang studi Matematika SMA-IPA nomor 16 sampai dengan nomor 20 tentang:

• sudut antara dua vektor, 
• proyeksi vektor, 
• transformasi geometri, 
• pertidaksamaan logaritma, dan 
• persamaan eksponen.

Soal No. 16 tentang Sudut antara Dua Vektor

Diketahui vektor-vektor

Nilai sinus sudut vektor u dan vektor v adalah ….

A.   −½
B.   0
C.   ½
D.   ½√2
E.   ½√3

Pembahasan

Kita tentukan dulu perkalian antara vektor u dan v serta panjang masing-masing vektor.

u ∙ v = 1 ∙ 1 + 0 ∙ (-1) + 1 ∙ 0
        = 1 + 0 + 0
        = 1

|u| = √(1² + 0² + 1²)
     = √2

|u| = √(1² + (−1)² + 0²)
     = √2

Sudut antara vektor u dan vektor v dirumuskan sebagai:

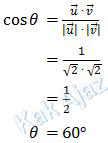
Dengan demikian,

sin⁡ θ = sin 60°
         = ½√3

Jadi, nilai sinus sudut vektor u dan vektor v adalah ½√3 (E).

Perdalam materi ini di Pembahasan Matematika IPA UN: Sudut antara Dua Vektor

Soal No. 17 tentang Proyeksi Vektor

Pembahasan

Perkalian vektor a dan b serta panjang vektor b adalah:

a ∙ b = −1 ∙ 1 + (−1) ∙ (−1) + 2 ∙ (−2)
        = −1 + 1 − 4
        = −4

|b| = √(1² + (−1)² + (−2)²)
     = √6

Misal vektor c adalah proyeksi vektor orthogonal a terhadap b, maka:

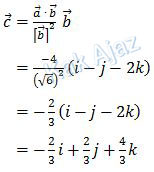
Jadi, proyeksi vektor orthogonal a pada b adalah −2/3 i + 2/3 j + 4/3 k (E).

Perdalam materi ini di Pembahasan Matematika IPA UN: Proyeksi Vektor

Soal No. 18 tentang Transformasi Geometri

Titik P(−3, 1) dipetakan oleh rotasi dengan pusat O sejauh 90° dilanjutkan dengan translasi . Peta titik P adalah ….

Artkel Terkait  Pembahasan Kimia UN 2015 No. 21

A.   P”(2, 1)
B.   P”(0, 3)
C.   P”(2, 7)
D.   P”(4, 7)
E.   P”(4, 1)

Pembahasan

Matriks transformasi untuk rotasi 90° adalah:

Bayangan titik P(−3,1) oleh transformasi R adalah:

Dengan demikian, bayangannya adalah P’(−1, −3). Selanjutnya titik P’ ini mengalami translasi T.

Jadi, peta titik P adalah P”(2, 1) (A).

Perdalam materi ini di Pembahasan Matematika IPA UN: Transformasi Geometri

Soal No. 19 tentang Pertidaksamaan Logaritma

Pembahasan

Rumus yang harus diingat adalah:

• log⁡ a + log ⁡b = log ⁡ab
• (a + b)(a − b) = a² − b²
• Jika ^alog⁡ f(x) ≤ ^alog⁡ g(x) maka f(x) ≤ g(x), untuk a > 1

Ok, mari kita selesaikan!

²log⁡(x + 2) + ²log⁡(x − 2) ≤ ²log⁡5
              ²log⁡(x + 2)(x − 2) ≤ ²log⁡5
                         ²log⁡(x² − 4) ≤ ²log⁡5

Karena bilangan pokok lebih dari 1 (a = 2) maka tanda pertidaksamaan tidak berubah.

x² − 4 ≤ 5
x² − 9 ≤ 0
(x + 3)(x − 3) ≤ 0

Pembuat nol x = −3, x = 3, dan tanda pertidaksamaannya “≤” sehingga intervalnya berada di antara pembuat nol.

−3 ≤ x ≤ 3

Jangan lupa syarat logaritma! Fungsi yang di-log harus positif.

x + 2 > 0
      x > −2

x − 2 > 0
      x > 2

Selanjutnya kita buat garis bilangan untuk ketiga pertidaksamaan di atas.

Himpunan penyelesaiannya adalah daerah yang diarsir.

2 < x ≤ 3

Jadi, himpunan penyelesaian pertidaksamaan logaritma di atas adalah {x│2 < x ≤ 3} (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Pertidaksamaan Eksponen dan Logaritma

Soal No. 20 tentang Persamaan Eksponen

Persamaan grafik fungsi seperti pada gambar berikut adalah ….

A.   y = 2^{½x − 1}
B.   y = 2^{−½x − 1)}
C.   y = 2^{x − 2}
D.   y = 2^{x + 2}
E.   y = 2^{2x − 1}

Pembahasan

Cara yang efektif untuk menyelesaikan soal di atas adalah dengan cara substitusi langsung ke opsi jawaban.

Pada grafik di atas, kurva melalui titik (2, 1) dan (4, 2). Artinya, jika kita substitusi x = 2 maka harus menghasilkan y = 1. Demikian juga jika kita substitusi x = 4 maka akan menghasilkan y = 2.

Mari kita mulai dari opsi A!

              y = 2^{½x − 1}
x = 2 → y = 2^{½∙2 − 1}
                 = 2
                 = 1 [benar]

x = 4 → y = 2^{½∙4 − 1}
                 = 2¹
                 = 2 [benar]

Ternyata jawabannya adalah A. Tumben ya, biasanya soal seperti ini jawabannya ditaruh di D atau E.

Jadi, persamaan grafik fungsi eksponen di atas adalah y = 2^{½x − 1} (A).

Simak Pembahasan Soal Matematika IPA UN 2013 selengkapnya.

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih