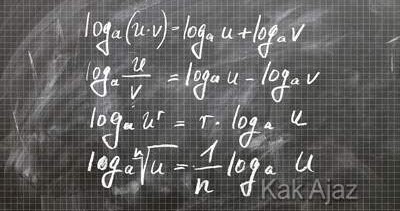Pembahasan Matematika IPA UN 2013 No. 1

Pembahasan soal-soal Ujian Nasional (UN) tahun 2013 bidang studi Matematika SMA-IPA nomor 1 sampai dengan nomor 5 tentang:

• penarikan kesimpulan, 
• ekuivalensi, 
• bentuk akar, 
• logaritma, dan 
• persamaan kuadrat.

Soal No. 1 tentang Penarikan Kesimpulan

Pembahasan

Kita misalkan terlebih dahulu.

p : Harga BBM naik
q : Harga sembako naik
r : tarif tol naik

Premis 1 dan 2 berbentuk implikasi (kalimat bersyarat). Kita selesaikan dulu dengan silogisme.

   p ⇒ q
   q ⇒ r
⎯⎯⎯⎯⎯
∴ p ⇒ r

Hasil kesimpulan kedua premis tersebut kita operasikan dengan premis 3 dengan modus Tollens.

     p ⇒ r
   ~r
⎯⎯⎯⎯⎯⎯
∴ ~p

Kesimpulan akhirnya adalah ~p. Karena p adalah ‘harga BBM naik’ maka ~p adalah ‘harga BBM tidak naik’.

Jadi, kesimpulan yang sah dari ketiga premis di atas adalah harga BBM tidak naik (D).

Soal No. 2 tentang Ekuivalensi

Pembahasan

Misal:

p : Ani mengikuti pelajaran matematika
q : Ani mendapat tugas menyelesaikan soal-soal matematika

Pernyataan “Ani tidak mengikuti pelajaran matematika atau Ani mendapat tugas menyelesaikan soal-soal matematika.” berbentuk disjungsi:

~p ∨ q

Pernyataan disjungsi mempunyai hubungan ekuivalensi dengan implikasi.

~p ∨ q ≡ p ⇒ q

Pernyataan p ⇒ q berarti “Jika Ani mengikuti pelajaran matematika maka Ani mendapat tugas menyelesaikan soal-soal matematika.”

Jadi, pernyataan yang setara adalah opsi (A).

Soal No. 3 tentang Bentuk Akar

Bentuk sederhana dari

Pembahasan

Penyederhanaan bentuk akar yang paling umum adalah dengan cara mengalikan bentuk sekawan.

Catatan:
Penyebut pecahan diselesaikan dengan rumus:

(a + b)(a − b) = a² − b²

Jadi, penyederhanaan bentuk akar tersebut yang paling tepat adalah opsi (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Bentuk Akar

Soal No. 4 tentang Logaritma

Diketahui ³log⁡ 5 = a dan ²log⁡ 3 = b. Nilai ⁶log⁡ 10 adalah ….

Pembahasan

Rumus-rumus yang perlu diingat untuk menyelesaikan soal di atas adalah:

Mari kita selesaikan dengan hati-hati!

Agar dapat diselesaikan, Kak Ajaz selipkan bilangan pokok yang sama, yaitu 3. Bilangan pokok ini diambil dari angka yang ada pada soal.

Jadi, nilai dari ⁶log⁡ 10 adalah opsi (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Logaritma

Soal No. 5 tentang Persamaan Kuadrat

Pembahasan

Diketahui:

α = 2β

Penjumlahan kedua akar persamaan kuadrat x² + (a − 1)x + 2 = 0 adalah:

α + β = −(a − 1)/1
α + β = 1 − a

Substitusi α = 2β diperoleh:

2β + β = 1 − a
         a = 1 − 3β       … (1)

Sedangkan perkalian kedua akarnya adalah:

α ∙ β = 2/1
α ∙ β = 2                   … (2)

Substitusi α = 2β diperoleh:

2β ∙ β = 2
     β² = 1
       β = ±1

Nah, sekarang Kak Ajaz substitusikan nilai β ini ke persamaan (1).

a = 1 − 3β
   = 1 − 3 ∙ (±1)
   = 1 ∓ 3

Berarti nilai a ada dua:

a = 1 − 3 = −2    dan
a = 1 + 3 = 4

Karena a > 0 maka yang memenuhi adalah a = 4.

Jadi, nilai a pada persamaan kuadrat tersebut adalah 4 (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Persamaan Kuadrat

Simak Pembahasan Soal Matematika IPA UN 2013 selengkapnya.

Pembahasan Matematika IPA UN 2013 No. 6 – 10
Pembahasan Matematika IPA UN 2013 No. 01 – 05

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih