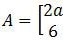pembahasan selanjutnya adalah
- matriks,
- persamaan dan fungsi kuadrat,
- grafik fungsi kuadrat,
- ukuran pemusatan, serta
- peluang kejadian.
Soal No. 56 tentang Matriks
Jika

merupakan matriks yang mempunyai invers maka jumlah semua nilai a yang mungkin sehingga det (−½ A) = det (A−1) adalah ….
A. 2
B. 4
C. 6
D. 8
E. 10
Pembahasan
Rumus determinan matriks yang perlu dikuasai untuk menjawab soal di atas adalah:
det (kA) = k2 det A
det A−1 = 1/(det A)
Determinan untuk matriks A di atas adalah:
det A = 2a − 6
Mari kita kerjakan soal di atas!
det (−½ A) = det (A−1)
(−½)2 det A = 1/(det A)
¼ det A = 1/(det A)
(det A)2 = 4
Sekarang kita masukkan det A = 2a − 6.
(2a − 6)2 = 4
4a2 − 24a + 36 = 4
4a2 − 24a + 32 = 0
a2 − 6a + 8 = 0
Karena berbentuk persamaan kuadrat, maka nilai a ada dua, yaitu a1 dan a2. Untuk mendapatkan jumlah nilai a, kita bisa menggunakan rumus jumlah akar-akar persamaan kuadrat.
a1 + a2 = −b/a [a = 1, b = −6]
= − (−6)/1
= 6
Jadi, jumlah semua nilai a yang mungkin adalah 6 (C).
Soal No. 57 tentang Persamaan dan Fungsi Kuadrat
A. −30
B. −11
C. 11
D. 25
E. 30

Pembahasan
Absis titik minimum fungsi kuadrat adalah sumbu simetri.
x = −b/2a [rumus sumbu simetri]
5/2 = −b/2 [a = 1]
b = −5
Untuk mendapatkan nilai c, kita substitusikan titik minimum (5/2, −1/4) dan b = −5 pada fungsi kuadrat tersebut.
y = x2 + bx + c
−1/4 = (5/2)2 + (−5)(5/2) + c
−1/4 = 25/4 −25/2 + c
−1 = 25 − 50 + 4c [kedua ruas dikalikan 4]
24 = 4c
c = 6
Dengan ditemukannya nilai b dan c, persamaan kuadrat tersebut menjadi:
y = x2 − 5x + 6
Grafik fungsi kuadrat tersebut melalui titik (p, 0) dan (q, 0). Kedua titik ini merupakan titik potong pada sumbu x atau pembuat nol fungsi sehingga p dan q merupakan akar-akar persamaan kuadrat tersebut.
Mari kita gunakan sifat penjumlahan dan perkalian akar-akar persamaan kuadrat.
p + q = −b/a [a = 1, b = −5]
= 5
p . q = c/a [a = 1, c = 6]
= 6
Dengan demikian, nilai dari p2q + pq2 adalah:
p2q + pq2 = pq(p + q)
= 6 × 5
= 30
Jadi, nilai dari adalah 30 (E).
Soal No. 58 tentang Grafik Fungsi Kuadrat
A. 2
B. 4
C. 6
D. 8
E. 9
Pembahasan
Grafik fungsi y = 4 − x2 memotong sumbu-x di titik A dan B.
y = 0
4 − x2 = 0
x2 = 4
x = ±2
∴ A(−2, 0) dan B(2, 0)
Grafik fungsi y = 4 − x2 memotong sumbu-y di titik C.
x = 0 → y = 4 − x2
y = 4 − 02
y = 4
∴ C(0, 4)
Perhatikan ilustrasi grafik yang dimaksud pada soal berikut ini!

Berdasarkan grafik di atas, luas segitiga ABC adalah:
L ΔABC = ½ × AB × OC
= ½ × 4 × 4
= 8
Jadi, luas segitiga ABC adalah 8 satuan luas (D).
Soal No. 59 tentang Ukuran Pemusatan
A. 2,4 juta rupiah
B. 3 juta rupiah
C. 3,6 juta rupiah
D. 6 juta rupiah
E. 9 juta rupiah
Pembahasan
Data-data yang diketahui pada soal:
nA = 20
nB = 40
xA = 2xB → xB = ½ xA
Total keuntungan agen A dan B sebesar 360 juta rupiah.
nA . xA + nB . xB = 360
20 . xA + 40 . ½ xA = 360
20xA + 20xA = 360
40xA = 360
xA = 9
Jadi, rata-rata keuntungan agen yang menjual produk A adalah 9 juta rupiah (E).
Soal No. 60 tentang Peluang Kejadian
A. 4/5
B. 2/3
C. 3/5
D. 1/2
E. 1/5
Pembahasan
Terdapat 6 buku, yaitu 4 buku Kombinatorika dan 2 buku Statistika disusun dengan tidak membedakan judul yang sama. Banyak semua kemungkinan (ruang sampel) dapat ditentukan dengan menggunakan permutasi dengan unsur yang sama.
n(S) = 6P(4, 2)

= 15
C adalah kejadian susunan buku sehingga terdapat tiga atau lebih buku dengan judul yang sama tersusun secara berurutan. Susunan yang mungkin adalah:
- KKKKSS [huruf bercetak merah diacak]
3!/2! = 3 [permutasi 3 dengan 2 unsur yang sama]
3!/2! = 3
- Tiga atau lebih buku Kombinatorika ada di tengah
- SKKKKS
- SKKKSK
- KSKKKS
Sehingga banyak kejadian C adalah:
n(C) = 3 + 3 + 3
= 9
Peluang kejadian C adalah:
P(C) = n(C)/n(S)
= 9/15
= 3/5
Jadi, peluang kejadian C adalah 3/5 (C).
Pembahasan Matematika Dasar No. 51 – 55 TKPA SBMPTN 2015
Simak juga:
Pembahasan Matematika Dasar No. 1 – 5 TKPA SBMPTN 2014
Pembahasan Matematika Dasar No. 46 – 50 TKPA SBMPTN 2016
Pembahasan Matematika Dasar No. 46 – 50 TKPA SBMPTN 2017
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat