pembahasan selanjutnya adalah
- geometri,
- statistika,
- limit fungsi,
- sistem persamaan linear, dan
- pertidaksamaan.
Soal No. 56 tentang Geometri
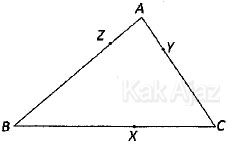
Jika BC, CA, dan AB berturut-turut adalah a cm, b cm, dan c cm, maka 2AY = … cm.
A. a + b + c
B. a − b + c
C. a + b − c
D. −a − b + c
E. b + c − a
Pembahasan
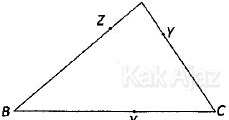
Perhatikan gambar berikut ini!
Misalkan:
AY = AZ = x
maka:
BX = BZ = c − x
CX = CA = b − x
Perhatikan sisi BC!
BC = BX + CX
a = c − x + b − x
a = b + c − 2x
2x = b + c − a
Ingat, x = AY. Sehingga:
2AY = b + c − a
Jadi, nilai dari 2AY adalah b + c − a (E).
Soal No. 57 tentang Statistika
A. 2
B. 3
C. 4
D. 6
E. 8
Pembahasan
Median adalah nilai tengah dari data yang telah diurutkan.
Perhatikan nilai 5 ujian yang telah diurutkan berikut ini:
4, 5, 6, 7, 8
Median dari 5 data tersebut adalah 6.
Misalkan nilai ujian ke-6 adalah x. Jika x adalah 1 sampai dengan 5 maka dapat diurutkan sebagai berikut:
x, 4, 5, 6, 7, 8
Median dari 6 data tersebut berada di antara 5 dan 6, yaitu 5,5.
Sementara itu, ketentuan pada soal adalah bahwa rata-rata dari 6 ujian lebih kecil dari mediannya.
Sedangkan jika x adalah 7 sampai 10 maka dapat diurutkan sebagai berikut:
4, 5, 6, 7, 8, x
Median dari ke-6 data tersebut berada di antara 6 dan 7, yaitu 6,5.
Nilai x yang mungkin bila rata-ratanya kurang dari median adalah:
Dengan demikian, nilai ulangan terakhir yang mungkin adalah:
1, 2, 7, atau 8 (ada 4 nilai)
Jadi, nilai ujian ke-6 yang mungkin ada sebanyak 4 (D).
Soal No. 58 tentang Limit Fungsi
Jika f(b + 1) = 0 dan
maka a + 2b = ….
A. −2
B. −1
C. 0
D. 1
E. 2
Pembahasan
Perhatikan limit fungsi yang tersaji pada soal!
Karena limit fungsi tersebut hasilnya ada, yaitu −1, maka dapat diterapkan aturan L’Hopital, yaitu pembilang dan penyebutnya masing-masing diturunkan.
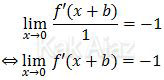
Sekarang perhatikan fungsi f.
f(x) = x2 + ax + b
f’(x) = 2x + a
f’(x + b) = 2(x + b) + a
= 2x + 2b + a
Nah, hasil f’(x + b) ini kita substitusikan ke limit di atas.
limx→0 f’(x + b) = −1
limx→0 2x + 2b + a = −1
Dengan memasukkan x = 0 diperoleh:
2b + a = −1
a + 2b = −1
Jadi, nilai dari a + 2b adalah −1 (B).
Soal No. 59 tentang Sistem Persamaan Linear
A. 8
B. 4
C. 3
D. −4
E. −3
Pembahasan
Diketahui sistem persamaan linear:
3x − 2y = −1 … (1)
−2x + 3y = 4 … (2)
4x + by = 4b … (3)
ax + 3y = 2a … (4)
Eliminasi persamaan (1) dan (2)
3x − 2y = −1 |×2| 6x − 4y = −2
−2x + 3y = 4 |×3| −6x + 9y = 12
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ +
5y = 10
y = 2
Substitusi y = 2 ke persamaan (1).
3x − 4 = −1
3x = 3
x = 1
Selanjutnya kita substitusikan x = 1 dan y = 2 ke persamaan (3) dan (4).
4x + by = 4b
4 + 2b = 4b
4 = 2b
b = 2
ax + 3y = 2a
a + 6 = 2a
a = 6
Dengan demikian:
a + b = 6 + 2
= 8
Jadi, nilai dari a + b adalah 8 (A).
Soal No. 60 tentang Pertidaksamaan
adalah ….
A. x < 0
B. 0 < x ≤ 2
C. 0 < x < 4
D. 2 ≤ x < 4
E. x > 4
Pembahasan
Perhatikan pertidaksamaan berikut ini!
Pada pertidaksamaan di atas terdapat fungsi harga mutlak yang bentuknya sama, yaitu |x − 2|.
Fungsi yang terdapat dalam harga mutlak tersebut bernilai nol dan positif bila x ≥ 2 dan bernilai negatif bila x < 2.
I. |x − 2| = x − 2 untuk x ≥ 2
II. |x − 2| = −x + 2 untuk x < 2
Mari kita terapkan dua ketentuan tersebut untuk menyelesaikan pertidaksamaan di atas.
I. Untuk x ≥ 2
Diperoleh: 2 ≤ x ≤ 4
Karena syarat penyebut x ≠ 4 maka:
2 ≤ x < 4 … (1)
II. Untuk x < 2
Diperoleh: 0 ≤ x ≤ 2
Karena syarat penyebut x ≠ 0 maka:
0 < x ≤2 …(2)
Penyelesaian akhir pertidaksamaan tersebut merupakan gabungan antara pertidaksamaan (1) dan (2). Diperoleh:
0 < x < 4
Jadi, bilangan real x yang memenuhi adalah 0 < x < 4 (C).
Pembahasan Matematika Dasar No. 51 – 55 TKPA SBMPTN 2016
Simak juga:
Pembahasan Matematika Dasar No. 1 – 5 TKPA SBMPTN 2014
Pembahasan Matematika Dasar No. 46 – 50 TKPA SBMPTN 2015
Pembahasan Matematika Dasar No. 46 – 50 TKPA SBMPTN 2017
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat