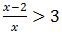Pembahasan Matematika Dasar No. 51

• pertidaksamaan, 
• fungsi dan komposisi fungsi, 
• sistem persamaan linear, 
• operasi aljabar, serta 
• invers fungsi.

Soal No. 51 tentang Pertidaksamaan

Himpunan penyelesaian pertidaksamaan

adalah ….

A.   {x ∈ R│x < 0}
B.   {x ∈ R│−1 < x < 0}
C.   {x ∈ R│0 < x < 1}
D.   {x ∈ R│x < −2 atau x > 1}
E.   {x ∈ R│x < −1 atau x > 0}

Pembahasan

Dalam menyelesaikan soal pertidaksamaan, jangan sekali-kali mengalikan silang, membagi, mengalikan dengan variabel, kecuali jika variabel tersebut definit positif. Penyelesaian yang paling aman adalah dengan memindah ruas.

Dalam pertidaksamaan pecahan, berlaku hubungan:

Jika a/b < 0 maka a.b < 0

Sehingga pertidaksamaan di atas menjadi: 

x(2x + 2) < 0

Pembuat nol pertidaksamaan tersebut adalah: 

x = 0
2x + 2 = 0 → x = −1

Karena koefisien kuadratnya positif (2x²) maka tanda “<” berarti penyelesaian pertidaksamaan tersebut berada di antara titik pembuat nol.

−1 < x < 0

Jadi, himpunan penyelesaian pertidaksamaan tersebut adalah opsi (B).

Soal No. 52 tentang Fungsi dan Komposisi Fungsi

Pembahasan

Data-data yang diketahui pada soal: 

f(−x) = −f(x) 
f(3) = −5 
f(−5) = 1

Sekarang kita langsung masuk ke pertanyaan. 

f(f(−3)) = f(−f(3))    [f(−x) = −f(x)]
             = −f(f(3))    [f(3) = −5]
             = −f(−5)      [f(−5) = 1]
             = −1

Jadi, nilai dari f(f(−3)) adalah −1 (C).

Soal No. 53 tentang Sistem Persamaan Linear

Diketahui sistem persamaan linear

Nilai x + y adalah ….

A.   −3
B.   −2
C.   −1
D.   3
E.   5

Pembahasan

Sistem persamaan linear di atas kita sederhanakan dengan mengalikan 6 pada masing-masing ruas.

3(x + 2) − 2(x − y) = 6
   3x + 6 − 2x + 2y = 6
                    x + 2y = 0      … (1)

2(x + y) − 3(y + 1) = 12
    2x + 2y − 3y − 3 = 12
                     2x − y = 15    … (2)

Sekarang kita eliminasi persamaan (1) dan (2). 

x + 2y = 0     |×2|  2x + 4y = 0
2x − y = 15   |×2|  2x −  y  = 15
                          —————— −
                                      5y = −15
                                        y = −3

Selanjutnya kita substitusi y = −3 ke persamaan (1). 

y = −3 → x + 2y = 0
                  x − 6 = 0
                        x = 6

Dengan demikian, 

x + y = 6 − 3
         = 3

Jadi, nilai dari x + y adalah 3 (C).

Soal No. 54 tentang Operasi Aljabar

Pembahasan

Empat orang siswa (A, B, C, dan D) akan mengikuti lomba karya inovatif dengan biaya Rp900.000,00. Biaya tersebut ditanggung bersama.

A + B + C + D = 900.000

Siswa A memberikan kontribusi setengah dari jumlah kontribusi tiga siswa lainnya.

  A = ½(B + C + D)
  A = ½(900.000 − A) [kedua ruas dikalikan 2]
2A = 900.000 − A
3A = 900.000
  A = 300.000

Siswa B memberikan kontribusi sepertiga dari jumlah kontribusi tiga siswa lainnya.

  B = ⅓(A + C + D)
  B = ⅓(900.000 − B)  [kedua ruas dikalikan 3]
3B = 900.000 − B
4A = 900.000
  A = 225.000

Siswa C memberikan kontribusi seperempat dari jumlah kontribusi tiga siswa lainnya.

  C = ¼(A + B + D)
  C = ¼(900.000 − C) [kedua ruas dikalikan 4]
4C = 900.000 − C
5C = 900.000
  C = 180.000

Dengan demikian, besar kontribusi siswa D adalah:

D = 900.000 − (A + B + C)
    = 900.000 − (300.000 + 225.000 + 180.000)
    = 900.000 − 705.000
    = 195.000

Jadi, besar kontribusi siswa D adalah Rp195.000,00 (C).

Soal No. 55 tentang Invers Fungsi

Jika

maka f⁻¹(x) = ….

Pembahasan

Langkah pertama adalah mengubah bentuk f(x + 2) menjadi bentuk f(x).

Selanjutnya kita tentukan invers fungsi f(x) dengan menggunakan rumus:

Dengan menggunakan rumus invers di atas, diperoleh:

Jadi, invers fungsi f adalah opsi (B).

Pembahasan Matematika Dasar No. 46 – 50 TKPA SBMPTN 2015
Pembahasan Matematika Dasar No. 56 – 60 TKPA SBMPTN 2015

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih