Pembahasan Matematika Dasar No. 51

• kaidah pencacahan, permutasi, dan kombinasi, 
• komposisi fungsi, 
• invers fungsi, 
• matriks, serta 
• barisan dan deret.

Soal No. 51 tentang Kaidah Pencacahan, Permutasi, dan Kombinasi

Pembahasan

Misalkan:

P    : finalis pria
W   : finalis wanita
P_A   : finalis pria dari SMA “A”
W_A : finalis wanita dari SMA “A”

Finalis pria dan wanita tampil bergantian serta finalis dari SMA “A” tidak tampil berurutan. Susunan yang mungkin adalah:

1. P_A W P W_A P W P
2. P_A W P W P W_A P
3. P W P_A W P W_A P
4. P W_A P W P_A W P
5. P W_A P W P W P_A
6. P W P W_A P W P_A

Sekarang perhatikan salah satu susunan tersebut, misal susunan yang pertama.

P_A W P W_A P W P

Dengan P_A dan W_A pada posisi yang tetap, 3 P dan 2 W bisa dipertukarkan. Sehingga banyak urutan yang mungkin adalah:

3! × 2! = 3 × 2 × 1 × 2 × 1
            = 12

Demikian juga dengan 5 susunan yang lain dapat diberlakukan seperti di atas. Sehingga banyak seluruh urutan susunan adalah:

6 × 12 = 72

Jadi, susunan urutan tampil yang mungkin ada sebanyak 72 (C).

Soal No. 52 tentang Komposisi Fungsi

Pembahasan

f(g(x)) berarti menggantikan x pada fungsi f dengan g(x).

          f(g(x)) > g(f(x))
     a g(x) − b > c f(x) + b
a(cx + b) − b > c(ax − b) + b
 acx + ab − b > acx − bc + b

acx pada ruas kiri dan kanan bisa dicoret. Sementara itu sisa suku yang lain masing-masing dibagi b. Diperoleh:

a − 1 > −c + 1
 a + c > 2

Jadi, syarat agar f(g(x)) > g(f(x)) adalah a + c > 2 (C).

Soal No. 53 tentang Invers Fungsi

Pembahasan

Modal utama menyelesaikan soal di atas adalah memahami konsep berikut ini.

Jika            y = f(x)
maka   f⁻¹(y) = x

Diketahui bahwa f(2x) = g(x − 3). Anggap saja keduanya sama dengan y.

y = f(2x)
y = g(x − 3)

Sekarang kita terapkan konsep di atas. Kita mulai dari fungsi yang kedua.

        y = g(x − 3)
g⁻¹(y) = x − 3
        x = g⁻¹(y) + 3 … (1)

Kita simpan dulu hasilnya. Kita lanjutkan menerapkan konsep di atas untuk fungsi yang pertama.

       y = f(2x)
f⁻¹(y) = 2x        … (2)

Selanjutnya kita substitusikan persamaan (1) ke persamaan (2).

f⁻¹(y) = 2[g⁻¹(y) + 3]
f⁻¹(y) = 2g⁻¹(y) + 6

Dengan menggantikan y dengan x diperoleh:

f⁻¹(x) = 2g⁻¹(x) + 6

Jadi, invers fungsi f adalah 2g⁻¹(x) + 6 (E).

Soal No. 54 tentang Matriks

Jika

maka det⁡ (P) = ….

A.   −3
B.   −2
C.   1
D.   2
E.   3

Pembahasan

Misalkan:

Sekarang kita terapkan data di atas untuk persamaan matriks yang pertama.

Diperoleh:

b = 1
d = 0

Dengan cara yang sama, persamaan matriks yang kedua menjadi:

Diperoleh:

a + b = −1
a + 1 = −1
      a = −2

c + d = 3
c + 0 = 3
      c = 3

Sehingga:

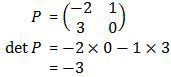
Jadi, determinan matriks P adalah 3 (A).

Soal No. 55 tentang Barisan dan Deret

Pembahasan

Cara 1

Rumus suku ke-k deret aritmetika dinyatakan

U_k = a + (k − 1)b

Berdasarkan rumus di atas maka:

U₂ = a + b
U₄ = a + 3b 
dan seterusnya

Dengan demikian,

U₂ + U₄ + U₆ + U₈ + U₁₀ + U₁₂ = 72
(a + b) + (a + 3b) + ⋯ + (a + 11b) = 72
6a + 36b = 72
    a + 6b = 12 … (1)

Sedangkan jumlah k suku pertama dirumuskan:

S_k = 1/2 k [2a + (k − 1)b]

Sehingga jumlah 13 suku pertama adalah:

S₁₃ = 1/2 × 13(2a + 12b)
S₁₃ = 13(a + 6b)              … (2)

Substitusi persamaan (1) ke persamaan (2) diperoleh:

S₁₃ = 13 × 12
S₁₃ = 156

Cara 2

Jumlah n suku barisan aritmetika yang berjarak tetap sama dengan perkalian antara banyak suku dan suku tengahnya (U_t).

S_n = n × U_t

Perhatikan penjumlahan suku yang tersaji pada soal di atas.

U₂ + U₄ + U₆ + U₈ + U₁₀ + U₁₂ = 72

Banyak suku yang dijumlahkan ada 6. Sedangkan suku tengah antara U₂ dan U₁₂ adalah U₇. Sehingga penjumlahan suku di atas menjadi:

6 × U₇ = 72
      U₇ = 12

Sekarang perhatikan pertanyaannya, yaitu S₁₃! Banyak suku yang dijumlah ada 13 sedangkan suku tengah antara U₁ dan U₁₃ adalah U₇. Sehingga:

S₁₃ = 13 × U₇
      = 13 × 12
      = 156

Jadi, jumlah 13 suku pertama barisan aritmetika tersebut adalah 156 (C).

Pembahasan Matematika Dasar No. 46 – 50 TKPA SBMPTN 2016
Pembahasan Matematika Dasar No. 56 – 60 TKPA SBMPTN 2016

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih