pembahasan selanjutnya adalah
- dinamika rotasi,
- titik berat,
- momen gaya,
- gerak menggelinding, dan
- elastisitas pegas.
Soal No. 6 tentang Dinamika Rotasi
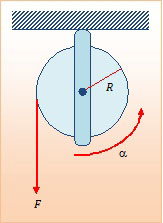
Gesekan katrol diabaikan. Jika momen inersia katrol I = β dan tali ditarik dengan gaya tetap F maka nilai F setara dengan ….
A. F = αβR
B. F = αβ2R
C. F = α(βR)−1
D. F = αβR−1
E. F = R(αβ)−1
Pembahasan
Karena katrol tersebut mempunyai percepatan (a) maka berlaku hukum II Newton. Hukum II Newton yang berlaku pada katrol adalah:
Στ = I α
FR = βα (I = β)
F = αβR−1
Jadi, nilai F setara dengan F = αβR−1 (D).
Soal No. 7 tentang Titik Berat
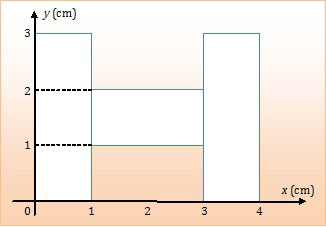
Koordinat titik berat bangun bidang tersebut adalah ….
A. (1½, 1½) cm
B. (2, ½) cm
C. (2, 1½) cm
D. (2½, 1½) cm
E. (2½, 2½) cm

Pembahasan
Ini soal pandangan mata. Hanya dipandang sudah terjawab. Bangun bidang tersebut benar-benar simetris, baik pada sumbu x maupun pada sumbu y. Sehingga letak titik berat benda tersebut tepat di tengah-tengah bangun.
Jadi, koordinat titik berat bangun bidang tersebut adalah (2, 1½) cm (C).
Perdalam materi ini di Pembahasan Fisika UN: Titik Berat.
Soal No. 8 tentang Momen Gaya
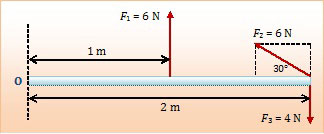
Besar resultan momen gaya terhadap poros titik O oleh gaya-gaya yang bekerja pada batang jika massanya diabaikan adalah ….
A. 7,5 Nm
B. 4 Nm
C. 3,5 Nm
D. 3 Nm
E. 2 Nm
Pembahasan
Anggap saja di titik O terdapat engsel yang dapat memutar batang 360°. Bila F1 dan F2 ditarik maka batang akan berputar berlawanan arah jarum jam. Sedangkan bila F3 ditarik maka batang akan berputar searah putaran jarum jam.
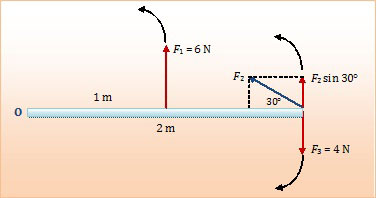
Karena F2 arahnya miring, terlebih dahulu kita proyeksikan ke arah vertikal menjadi F2 sin 30°.
Jika putaran yang berlawanan jarum jam kita anggap positif dan putaran yang searah jarum jam kita anggap negatif, besar resultan momen gaya di titik O adalah:
Στ = F1R1 + F2 sin 30° R2 − F3R3
= 6 × 1 + 6 × ½ × 2 − 4 × 2
= 4
Jadi, besar resultan momen gaya terhadap titik poros O oleh gaya-gaya yang bekerja pada batang adalah 4 Nm (B).
Perdalam materi ini di Pembahasan Fisika UN: Momen Gaya.
Soal No. 9 tentang Gerak Menggelinding
A. 9,5 m
B. 10,5 m
C. 11,5 m
D. 12,5 m
E. 13,5 m
Pembahasan
Perhatikan ilustrasi dari soal tersebut!

Sebuah silinder diberi kecepatan awal vo sehingga dapat mendaki bidang miring sampai sejauh s. Ketika mencapai jarak s, silinder berhenti (vt = 0). Percepatan gerak menggelinding dirumuskan;
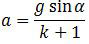
dengan k adalah konstanta momen inersia ( I = ½ mR2 berarti k = ½). Sehingga percepatan geraknya adalah:
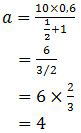
Rumus yang berkenaan dengan permasalahan tersebut adalah :
vt2 = vo2 − 2 as
0 = 102 − 2 × 4 × s
8 s = 100
s = 12,5
Jadi, panjang lintasan bidang miring yang ditempuh silinder sebelum berhenti adalah 12,5 m (D).
Soal No. 10 tentang Elastisitas Pegas

Berdasarkan grafik, pegas tetap akan bersifat elastis pada gaya tarik sebesar ….
A. 0 sampai 4 N
B. 0 sampai 8 N
C. 0 sampai 12 N
D. 8 N sampai 12 N
E. 8 N sampai 16 N
Pembahasan
Penjelasan grafik di atas adalah sebagai berikut.
- 0 – 8 N adalah daerah elastisitas atau daerah hukum Hooke yang digambarkan dengan garis lurus (linear). Cirinya mempunyai perbandingan ΔF terhadap Δx yang sama.
- 12 N adalah batas elastisitas, artinya kurang dari 12 N masih elastis, lebih dari 12 N tidak elastis.
- 12 N – 16 N adalah daerah plastis, artinya pegas dapat mengalami pertambahan panjang tetapi tidak bisa kembali ke keadaan semula (tidak elastis).
- 16 N adalah titik patah, artinya pegas tidak akan mengalami pertambahan panjang, jika dipaksakan akan putus.
Jadi, benda tetap akan bersifat elastis pada gaya tarik antara 0 – 12 N (C).
Perdalam materi ini di Pembahasan Fisika UN: Elastisitas Bahan.
Simak Pembahasan Soal Fisika UN 2014 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat