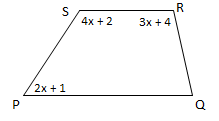Contoh Soal & Pembahasan Segi Empat Tingkat SMP

Jenis-Jenis Segi Empat

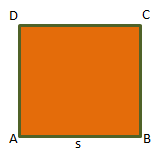
Persegi

Persegi merupakan segi empat yang memiliki panjang sisi yang sama besar dengan empat sudut siku-siku.

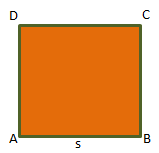
Rumus-rumus yang berlaku pada persegi, yaitu:

S = sisi-sisi persegi

Luas persegi = L = s x s = s²

Keliling persegi = K = 4 x s

Persegi memiliki sifat-sifat sebagai berikut:

1. Memiliki 4 simetri lipat , 4 simetri putar, dan 4 sumbu simetri
2. Keempat sisi panjangnya sama besar
3. Sudut di keempat sisi 90⁰ (siku-siku)
4. Diagonal-diagonalnya sama panjang
5. Menempati bingkai dengan 8 cara
6. Diagonal saling berpotongan tegak lurus dan membagi persegi sama panjang
7. Sisi-sisi yang saling berhadapan sejajar

Persegi panjang

Persegi panjang merupakan segi empat yang keempat sudutnya siku-siku dengan sisi-sisi yang berhadapan sama besar dan sejajar.

Rumus-rumus yang berlaku pada persegi panjang, yaitu:

p = panjang

l = lebar

Luas = L = p x l

Keliling = K = p + l + p + l = 2(p + l)

Persegi panjang memiliki sifat-sifat sebagai berikut:

1. Memiliki 2 simetri lipat, 2 simetri putar, dan 2 sumbu simetri
2. Sisi yang berhadapan sejajar dan sama panjang
3. Sudut di keempat sisi 90⁰ (siku-siku)
4. Diagonal-diagonalnya sama panjang
5. Menempati bingkai dengan 4 cara
6. Diagonal-diagonal yang saling berpotongan membagi dua bagian sama panjang

Jajar genjang

Jajar genjang merupakan segi empat dengan sisi-sisi yang berhadapan sejajar dan sama panjang.

Rumus-rumus yang berlaku pada jajar genjang, yaitu:

a = alas

t = tinggi

Dengan alas dan tinggi yang tegak lurus

Luas = L = a x t

Keliling = K = jumlah panjang semua sisi jajar genjang

Jajar genjang memiliki sifat-sifat sebagai berikut:

1. Hanya memiliki 2 simetri putar, tidak memiliki simetri lipat dan sumbu simetri
2. Jumlah semua sudut 360
3. Sisi yang saling berhadapan sejajar dan sama panjang
4. Sudut-sudut yang saling berhadapan sama besar
5. Diagonal saling berpotongan, membagi dua bagian sama besar dan membagi dua panjang sama panjang
6. Terbentuk dari sebuah segitiga dan bayangannya
7. Jumlah pasangan sudut yang saling berdekatan 180

Trapesium

Trapesium merupakan segi empat yang hanya memiliki sepasang sisi sejajar.

Trapesium memiliki sifat-sifat sebagai berikut:

• Memiliki 4 sisi dan 4 titik sudut
• Memiliki sepasang sisi yang sejajar tetapi tidak sama panjang
• Jumlah sudut yang berdekatan antara dua sisi sejajar adalah 180⁰
• Memiliki 1 simetri lipat dan 1 sumbu simetri terutama pada trapesium sama kaki

Trapesium dibagi menjadi 3 jenis, yaitu:

1. Trapesium sembarang
   Trapesium sembarang adalah trapesium dengan ukuran sisi yang berbeda-beda dan hanya memiliki 1 simetri putar
   

2. Trapesium siku-siku
   Trapesium siku-siku adalah trapesium yang memiliki dua sudut siku-siku dan hanya memiliki 1 simetri putar.
   

3. Trapesium sama kaki
   Trapesium sama kaki adalah trapesium yang memiliki sepasang rusuk yang sejajar dan sama panjang. Trapesium ini hanya memiliki 1 simetri lipat dan 1 simetri putar.
   

Rumus yang berlaku , yaitu:

Luas = L = ½ x jumlah dua sisi yang sejajar x tinggi = ½ (CD x AB x t)

Keliling = K = jumlah panjang semua sisi trapesium = AB + BC + CD + DA

Belah ketupat

Belah ketupat merupakan segi empat yang memiliki empat buah rusuk yang memiliki panjang yang sama dan memiliki dua pasang sudut yang berhadapan sama besar. Belah ketupat terbentuk dari dua buah segitiga sama kaki yang memiliki ukuran yang identik.

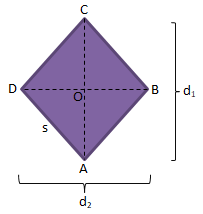
Rumus-rumus yang berlaku pada belah ketupat, yaitu:

d = diagonal

s = sisi-sisi

Luas = L = ½ x d₁ x d₂

Keliling = K = 4 x s

Belah ketupat memiliki sifat-sifat sebagai berikut:

• Memiliki empat sisi yang sejajar, berpasangan, dan sejajar
• Sudut-sudut yang berhadapan sama besar
• Dua diagonal berpotongan tegak lurus, sama panjang, dan membagi dua bagian sama besar
• Memiliki 2 simetri lipat, 2 simetri putar dan 2 sumbu simetri

Layang-layang

Layang-layang merupakan segi empat yang memiliki dua pasang sisi yang sama panjang tetapi tidak sejajar.

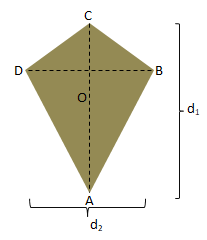
Rumus-rumus yang berlaku pada layang-layang, yaitu:

d = diagonal

s = sisi-sisi

Luas = L = ½ x d₁ x d₂

Keliling = K = jumlah semua panjang sisi-sisi layang-layang

Layang-layang memiliki sifat-sifat sebagai berikut:

• Memiliki 1 simetri lipat dan 1 sumbu simetri
• Memiliki dua pasang sisi yang berdekatan sama panjang
• Diagonal-diagonalnya saling tegak lurus, sama panjang, dan membagi dua bagian sama besar
• Sepasang sudut yang berhadapan sama besar
• Diagonal membagi dua sudut sama besar

Soal No.1

Persegi panjang ABCD dengan panjang AB = 30 cm dan BC = 24 cm. Titik O merupakan titik perpotongan  diagonal AC dan BD. Maka panjang OD adalah… cm.

1. 25
2. 30
3. 35
4. 40

PEMBAHASAN :

Jawaban B

”

Soal No.2

Persegi panjang ABCD memiliki keliling 58 cm. Jika selisih panjang dengan lebarnya adalah 5 cm, Maka luas persegi panjang ABCD adalah …..

1. 135 cm²
2. 212 cm²
3. 267 cm²
4. 311 cm²

PEMBAHASAN :
Diketahui:
Keliling (K) = 48
K = 48 = 2(p + l)
48 = 2(p + l)
p + l = 24…(i)
Diketahui selisih panjang dan lebar adalah 6
p – l = 6
p = l + 6…(ii)

Persamaan I disubsitusikan ke persamaan II
p + l = 24
(l + 6) + l = 24
2l + 6 = 24
2l = 18
l = 9 cm
Maka p = 9 + 6 = 15 cm.
Sehingga luasnya
L = p x l = 15 x 9 = 135 cm².
Jawaban B

Soal No.3

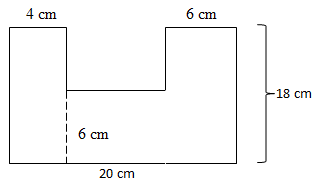
Maka luas bangun tersebut adalah . . . cm²

1. 210
2. 231
3. 324
4. 412

PEMBAHASAN :
Bangun tersebut terdiri dari tiga persegi panjang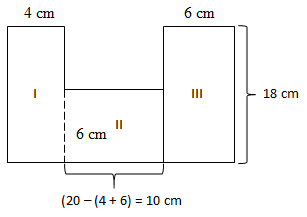

Luas total = Luas I + Luas II + Luas III
L = (4 x 6) cm² + (6 x 20) cm² + (18 x 10) cm² = 24 + 120 + 180 = 324 cm²
Jawaban C

Soal No.4
Ayah membeli sebidang tanah yang memiliki bentuk persegi dengan panjang sisi 12 m. Penjual menghargainya per m² adalah Rp. 3.000.000,00. Maka Ayah harus membayar tanah tersebut sebanyak…

1. Rp. 432.000.000,00
2. Rp. 450.000.000,00
3. Rp. 475.000.000,00
4. Rp. 535.100.000,00

PEMBAHASAN :
Menentukan luas tanah
Luas tanah = s² = 12 m x 12 m = 144
Maka Ayah harus membayar sebanyak  144 m² x Rp 3.000.000,00= Rp. 432.000.000,00
Jawaban A

Soal No.5

Sebuah rumah yang akan dipasang lantai. Ruangan yang akan dipasang lantai berukuran 6 m x 9 m dipasang ubin berukuran 30 cm x 30 cm. Maka jumlah ubin yang diperlukan untuk dipasang di ruangan tersebut adalah…

1. 432
2. 500
3. 600
4. 825

PEMBAHASAN :
Luas lantai ruangan yang akan dipasang ubin = 6 m x 9 m= 54 m² = 540.000 cm²
Luas untuk satu ubin = 30 cm x 30 cm = 900 cm²
Maka jumlah ubin yang perlukan adalah 540.000 : 900 = 600 buah.
Jawaban C

Soal No.6

Sebuah jajargenjang ABCD dengan Panjang AB  = (x+4) cm, BC = (3x+1) cm, jika diketahui  kelilingnya adalah 90 cm. Maka nilai x adalah …cm.

1. 10
2. 11
3. 12
4. 13

PEMBAHASAN :
Diketahui:
Keliling (K) = 90 cm
K = 2 (AB + BC) = 90 cm
2(x + 4) + 2(3x + 1) = 90
2x + 8 + 6x + 2 = 90
8x + 10 = 90
8x = 80
x = 10
Jawaban A

Soal No.7

Panjang diagonal belah ketupat PQRS adalah PR = 24 cm dan  QR = 50 cm. Maka keliling belah ketupat tersebut adalah….

1. 50
2. 75
3. 100
4. 125

PEMBAHASAN :
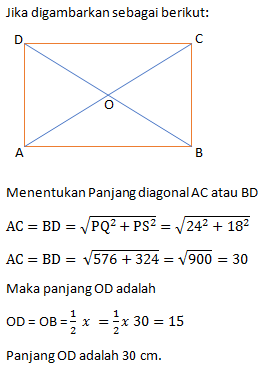
Jika digambarkan sebagai berikut.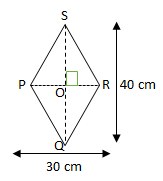

Keliling (K) belah ketupat PQRS = 4 PQ.
Menentukan PQ
OP = ½ x 30 = 15 cm
OQ = ½ x 40 = 20 cm
Maka PQ

Maka kelilingnya adalah
4 x 25 = 100 cm²
Jawaban C

Soal No.8

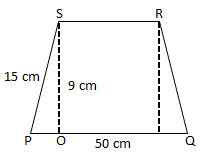
Jika diketahui trapesium PQRS maka luas trapesium tersebut adalah…cm²

PEMBAHASAN :
Diketahui:
tinggi trapesium (t) = 9 cm
Menentukan PO

Menentukan RS
RS = PQ – (2xPO) = 30 – (12×2) = 50 – 24 = 26 cm
Maka luas trapesium tersebut adalah
L = ½ (PQ + RS) x t = ½ (50 + 26) x 9 = 342 cm²
Jawaban A

Soal No.9

Diketahui perbandingan luas dua layang-layang X dan Y adalah 1 : 2 Jika panjang diagonal I layang-layang X dan Y adalah sama. Maka perbandingan panjang diagonal II layang-layang X dan Y adalah…

PEMBAHASAN 
Diketahui Perbandingan luas layang-layang X dan Y adalah 1 : 2 sehingga
L_Y = 2 L_X^.
Misal:
diagonal I = a
diagonal II = b maka:
L_X = ½ x a x b_X
L_Y = ½ x a x b_Y
Sehingga:
L_Y = 2 L_X
½ a b_Y = 2 x ½ d b_X
b_Y = 2b_X
Maka perbandingan perbandingannya adalah 1 : 2
Jawaban D

Soal No.10

Diketahui trapesium PQRS

maka ∠QRS adalah…

1. 92,5^o
2. 100^o
3. 105,5^o
4. 125^o

PEMBAHASAN :
∠QPS +∠PSR = 180^o
(2x + 1)+(4x + 2) = 180^o
6x + 3 = 180^o
6x = 177
x = 29,5^o
Maka,  ∠QRS = 3x + 4 = 3.29,5+ 4 = 92,5^o
Jawaban A

Soal No.11

Sebuah persegi panjang dengan ukuran panjang = 4p dan lebar = 3l. Ukuran persegi panjang tersebut kemudian diperbesar menjadi 3 kali lipatnya sehingga perbandingan luas persegi panjang semula dengan perbesarannya adalah …

1. 1 : 9
2. 2 : 3
3. 4 : 1
4. 1 : 2

PEMBAHASAN :
Diketahui:
Ukuran mula-mula:
Panjang = 4p
Lebar = 3l
Luas = p x l = 4p x 3l = 12pl

Ukuran diperbesar:
Panjang = 4p x 3 = 12p
Lebar = 3l x 3 = 9l
Luas = p x l  =12p x 9l = 108pl

Maka perbandingan luas persegi panjang sebagai berikut:
Luas mula-mula : Luas diperbesar
12pl : 108pl
1 : 9
Jawaban A

Soal No.12

Suatu persegi panjang dengan perbandingan panjang dan lebar adalah 4 : 3 dan kelilingnya sebesar 72 cm. Luas persegi panjang tersebut adalah … cm² .

1. 202,5
2. 235,71
3. 300
4. 303,75

PEMBAHASAN :
Diketahui:
Perbandingan panjang dan lebar = 5 : 3
Keliling = 72 cm
K = 2 x (p + l)
72 = 2 x (p + l)
P + l = 36

Menentukan besar panjang dan lebar sebagai berikut:

Maka luas persegi panjang sebagai berikut:
L = p x l = 22,5 cm x 13,5 cm = 303,75 cm²
Jawaban D

Soal No.13

Terdapat dua buah persegi, panjang sisi persegi P = ½ panjang sisi Q. Maka perbandingan luas persegi P dan Q adalah …

1. 1 : 4
2. 1 : 3
3. 1 : 2
4. 1 : 1

PEMBAHASAN :
Diketahui:
Panjang sisi persegi P = ½ Q
Luas persegi = sisi x sisi = s²

Maka perbandingan luas persegi P dan Q:

Jawaban A

Soal No.14

Pernyataan di bawah ini adalah sifat-sifat persegi, kecuali …

1. Memiliki 4 sumbu simetri
2. Setiap sudutnya membentuk sudut siku-siku
3. Memiliki dua buah diagonal yang sama panjang, berpotongan tidak membentuk siku-siku
4. Sisi yang berhadapan sama panjang

PEMBAHASAN :
Sifat-sifat persegi:

• Memiliki 4 sumbu simetri
• Setiap sudutnya membentuk sudut siku-siku
• Memiliki dua buah diagonal yang sama panjang, berpotongan di tengah-tengah, dan membentuk siku-siku
• Sisi yang berhadapan sama panjang

Jawaban C

Soal No.15

Panjang sisi sebuah persegi jika keliling dan luas persegi  4 : 7 adalah … cm.

1. 10
2. 9
3. 8
4. 7

PEMBAHASAN :
Diketahui:
Perbandingan keliling dan luas persegi = 4 : 7
K = 4s
L = s²

Maka panjang sisi persegi dapat dihitung sebagai berikut:

Jawaban D

Soal No.16

Sebuah persegi luasnya setengah dari luas persegi panjang. Persegi panjang tersebut berukuran 18 cm x 36 cm. Maka panjang sisi persegi adalah … cm.

1. 18 cm
2. 16 cm
3. 14 cm
4. 12 cm

PEMBAHASAN :
Diketahui:
Panjang persegi panjang = 18 cm
Lebar persegi panjang = 36 cm

Menentukan luas persegi panjang sebagai berikut:
L persegi panjang = p x l = 18 cm x 36 cm = 648 cm²

Menentukan luas persegi sebagai berikut:
L persegi = ½ x L persegi panjang = ½ x 648 cm²  = 324 cm²

Menentukan panjang sisi persegi sebagai berikut:
L persegi = s²
324   = s²
s = = 18 cm
Jawaban A

Soal No.17

Perhatikan gambar di bawah ini!

Halaman sebuah rumah berbentuk seperti gambar di atas. Maka luas halaman tersebut adalah …m² .

1. 178
2. 201
3. 245
4. 270

PEMBAHASAN :
Halaman I:
Panjang = 6 cm + 8 cm = 14 cm
Lebar = 3 m + 5 m = 8 m
Luas I = 14 m x 8 m = 112 m²

Halaman II:
Panjang = 8 m
Lebar = 8 m
Luas II = 8 m x 8 m = 64 m²

Halaman III:
Panjang = 5 m
Lebar = 5 m
Luas III = 5 m x 5 m = 25 m²

Maka luas halaman seluruhnya = 112 m² + 64 m² + 25 m²  = 201 m²
Jawaban B

Soal No.18

Perhatikan gambar berikut!

Besar ∠POS = …

1. 48⁰
2. 52⁰
3. 65
4. 70

PEMBAHASAN :
Diketahui:
∠POQ = 15x + 8
∠QOR = 6x + 4

Sudut-sudut yang bertolak belakang, berlaku:
∠POS = ∠QOR
∠POQ = ∠ROS

Menentukan nilai x sebagai berikut:
∠POQ + ∠QOR = 180⁰
(15x + 8) + (6x + 4) = 180
21x + 12 = 180⁰
21x = 168
x = 8

maka besar ∠POS = ∠QOR = 6x + 4 = 6(8) + 4 = 52
Jawaban B

Soal No.19

Perhatikan gambar di bawah ini!

Luas jajargenjang PQRS adalah … cm² .

1. 455,3
2. 522,5
3. 555,4
4. 580,9

PEMBAHASAN :
Menentukan tinggi ST sebagai berikut:

Maka luas jajargenjang PQRS = ST x (PT + SU)
.                                                     = 13,75 cm x (6 cm + 32  cm)
.                                                      = 13,75 cm x 38 cm
.                                                      = 522,5 cm²
Jawaban B

Soal No.20

Perhatikan gambar di bawah ini!

Besar  ∠BAD adalah … ⁰

1. 45
2. 58⁰
3. 67
4. 72

PEMBAHASAN :
Diketahui:
∠BAD = 3x – 5
∠ABD = 6x – 4

Menentukan nilai x, sebagai berikut:
∠BAD + ∠ABD = 180⁰
(3x – 5) + (6x – 4) = 180⁰
9x – 9 = 180⁰
9x = 189
x = 21

Maka besar ∠BAD
∠BAD = 3x – 5
∠BAD = 3(21) – 5 = 58
Jawaban B

Soal No.21

Pernyataan di bawah ini merupakan sifat-sifat bangun belah ketupat, kecuali …

1. Diagonal saling membagi dua bagian sama panjang
2. Memiliki empat simetri putar
3. Memiliki 4 buah simetri
4. Panjang sisi yang saling berhadapan sama besar

PEMBAHASAN :
Sifat-sifat belah ketupat adalah:

• Panjang sisi yang saling berhadapan sama besar
• Memiliki dua simetri lipat
• Diagonal berpotongan saling tegak lurus
• Diagonal merupakan sumbu simetri
• Memiliki empat sisi yang sama panjang
• Memiliki 4 simetri putar

Jawaban C

Soal No.22

Sebuah belah ketupat dengan keliling 96 cm, maka panjang sisi belah ketupat tersebut adalah … cm.

1. 20
2. 24
3. 27
4. 30

PEMBAHASAN :
Diketahui:
K = 96 cm

Maka keliling belah ketupat sebagai berikut:
K = 4s
96 cm = 4s
s = 24 cm
Jawaban B

Soal No.23

Perhatikan gambar berikut ini!

Besar keliling jajargenjang tersebut = … cm.

1. 45
2. 50
3. 59
4. 65

PEMBAHASAN :
Diketahui:
RS = 12 cm
QT = 7 cm
RT = 16 cm

Keliling jajargenjang PQRS = PQ + QR + RS + SP
SP = QR
PQ = RS

Maka keliling jajargenjang = 12 + 17,5 + 12 + 17,5 = 59 cm
Jawaban C

Soal No.24

Perhatikan gambar berikut ini!

Luas bangunan KLMNOP adalah … cm² .

1. 625,4
2. 691,6
3. 712,5
4. 735,7

PEMBAHASAN :
Diketahui:
Bangun KLMNOP = bangun jajargenjang
LM = 26 cm
KP = 15 cm
NQ = 7cm
NO = KP = KL = MN = 15 cm
OQ = MQ

Menentukan panjang OQ (tinggi jajargenjang) sebagai berikut:

Menentukan luas jajargenjang KLMN sebagai berikut:
Jajargenjang KLMN = jajargenjang KNOP
Luas KLMN = alas x tinggi
.                      =  26 cm x 13,3 cm
.                      = 345,8 cm²

Maka luas jajargenjang KLMNOP = 2 x luas KLMN
.                                                             = 2 x 345,8 cm²
.                                                             = 691,6 cm²
Jawaban B

Soal No.25

Perhatikan gambar berikut ini!

Luas trapesium PQRST = … cm² .

1. 342
2. 325
3. 311
4. 300

PEMBAHASAN :
Diketahui:
PS = 16 cm
RT = 6 cm
RS = 18 cm
PS = QT = 16 cm
QR = QT + TR
.     = 16 cm + 6 cm
.     = 22 cm

Maka luas trapesium PQRST adalah:
L = ½ x (PS + QR) x RS
.  = ½ x (16 cm + 22 cm) x 18 cm
.  = ½ x 38 cm x 18 cm
.  = 342 cm²
Jawaban A

Soal No.26

Pembuatan kerajinan berbentuk layang-layang dengan panjang diagonal 30cm dan 45cm. kemudian kerangka layang-layang tersebut akan ditutup dengan kertas berwarna berukuran 55cm x 55cm. kelebihan kertas yang terbuang adalah … cm² .

1. 2.555
2. 2.895
3. 2.490
4. 2.350

PEMBAHASAN :
Diketahui:
Panjang diagonal layang-layang = 30cm dan 45cm
Ukuran kertas = 55cm x 55cm

Menentukan luas layang-layang sebagai berikut:
L = ½ x diagonal layang-layang = ½ x 30cm x 45cm
L = ½ x 1.350cm² = 675cm²

Menentukan luas kertas sebagai berikut:
L = 55cm x 55cm = 3.025cm²

Maka sisa kelebihan kertas = 3.025cm² – 675cm² = 2.350cm²
Jawaban D

Soal No.27

Perhatikan gambar berikut!

Keliling layang-layang PQRS = … cm

1. 50
2. 55
3. 65
4. 80

PEMBAHASAN :
Diketahui:
OS = 8 cm
OQ = 17 cm
OR = OP = 10 cm
PQ = QR
PS = RS

Menentukan nilai QR sebagai berikut:

Menentukan nilai RS sebagai berikut:

Maka keliling PQRS adalah sebagai berikut:
K = PQ + QR + RS + PS
K = 19,7 cm + 19,7 cm + 12,8 cm + 12,8 cm = 65 cm
Jawaban C

Soal No.28

Perhatikan gambar berikut!

Luas belah ketupat KLMN = … cm² .

1. 515,7
2. 611,8
3. 614,4
4. 655,2

PEMBAHASAN :
Diketahui:
OM = 16 cm
MN = 25 cm

Menghitung panjang ON sebagai berikut:

Menentukan luas belah ketupat KLMN sebagai berikut:
KM = 2 x OM = 2 x 16 cm = 32 c
LN = 2 x ON = 2 x 19,2 cm = 38,4 cm
L = ½ x KM x LN
L = ½ x 32 cm x 38,4 cm = 614,4 cm²
Jawaban C

Soal No.29

Perhatikan gambar berikut!

Diketahui ∠EAD = 50⁰ , maka ∠ADC = …

1. 50
2. 60
3. 70
4. 80

PEMBAHASAN :
Menentukan ∠ADE sebagai berikut:
Jumlah sudut segitiga = 180⁰
∠EAD + ∠AED + ∠ADE = 180
50⁰ + 90⁰ + ∠ADE = 180
∠ADE = 180⁰ – 140
∠ADE = 40
Maka besar ∠ADC = 2 x 40⁰ = 80
Jawaban D

Soal No.30

Perhatikan gambar berikut!

Panjang QU adalah … cm.

1. 12,9
2. 13,2
3. 14,1
4. 14,8

PEMBAHASAN :
Diketahui:
PQ = 20 cm
PS = QR = 12 cm
RT = 8 cm

Menentukan panjang QT sebagai berikut:

Menentukan luas jajargenjang PQRS sebagai berikut:
Luas jajargenjang = PQ x QT = 20 cm x 8,9 cm = 178 cm²
Luas jajargenjang juga berlaku sebagai berikut:
PS x QU = PQ x QT
12 cm x QU = 178 cm²
QU = 14,8 cm
Jawaban D

Soal No.31

Bangun trapesium adalah bangun segi empat yang juga memiliki empat sudut. Khususnya pada trapesium bisa terdapat 2 atau 3 macam sudut sekaligus yaitu, kecuali …

1. Sudut lancip
2. Sudut tumpul
3. Sudut refleks
4. Sudut siku-siku

PEMBAHASAN :
Terdapat hal menarik pada sudut-sudut bangun trapesium yaitu bisa terdapat dua atau tiga macam sudut sekaligus yaitu sudut lancip (<90⁰ ), sudut siku-siku (90⁰ ), dan sudut tumpul (>90⁰ ).
Jawaban C

Soal No.32

Trapesium sama kaki memiliki sifat sebagai berikut …

1. Memiliki dua simetri putar
2. Memiliki satu simetri lipat
3. Tidak memiliki simetri lipat
4. Memiliki ukuran rusuk yang berbeda

PEMBAHASAN :
Sifat-sifat trapesium sama kaki adalah:

• Memiliki sepasang rusuk yang ukurannya sama panjang
• Sudut yang bersebelahan memiliki ukuran yang sama
• Hanya memiliki 1 simetri lipat dan 1 simetri putar

Jawaban B

Soal No.33

Sebuah belah ketupat ABCD memiliki luas 560 cm² .Panjang DB adalah 52 cm, maka panjang sisi belah ketupat ABCD adalah … cm.

1. 25
2. 28
3. 30
4. 32

PEMBAHASAN :

Diketahui:
L = 560 cm²
DB = 52 cm
AB = BC = CD = DA

Menghitung panjang AC sebagai berikut:
L = ½ x DB x AC
560 cm² = ½ x 52 cm x AC
AC = 21,5 cm

Maka panjang sisi belah ketupat ABCD sebagai berikut:
OB = ½ x DB = ½ x 52 cm = 26 cm
OC = ½ x AC = ½ x 21,5 cm = 10,75 cm

Jawaban B

Soal No.34

Perhatikan gambar di bawah ini!

Luas belah ketupat PQRS = … cm² .

1. 240
2. 280
3. 340
4. 380

PEMBAHASAN :
Diketahui:
OQ = 17 cm
OR = 10 cm
PR = 2 x OR = 2 x 10 cm = 20 cm
SQ = 2 x OQ = 2 x 17 cm = 34 cm

Maka, luas belah ketupat PQRS dapat dihitung sebagai berikut:
L = ½ x PR x SQ
L = ½ x 20 cm x 34 cm
L = 340 cm²
Jawaban C

Soal No.35

Perhatikan gambar di bawah ini!

Besar keliling jajargenjang tersebut = … cm.

1. 98
2. 100
3. 59
4. 65

PEMBAHASAN :
Diketahui:
AB = DC = 32 cm
BE = 8 cm
CE = 15 cm
BC = DA

Keliling jajargenjang ABCD = AB + BC + CD + DA

Maka keliling jajargenjang = 32 + 17 + 32 + 17 = 98 cm
Jawaban A

Soal No.36

Perhatikan gambar di bawah ini!

Luas layang-layang ABCD adalah … cm² .

1. 136,2
2. 137,5
3. 140,6
4. 142,2

PEMBAHASAN :
Diketahui:
CD = 9 cm
OC = OA = 6 cm
OB = 16 cm

Menentukan panjang OD sebagai berikut:

Maka luas layang-layang ABCD dapat dihitung sebagai berikut:
AC = OC + OA = 6 cm + 6 cm = 12 cm
BD = OB + OD = 16 cm + 6,7 cm = 22,7 cm
L = ½ x AC x BD
L = ½ x 12 cm x 22,7 cm
L = 136,2 cm²
Jawaban A

Soal No.37

Perhatikan gambar di bawah ini!

Besar ∠BCD adalah …

1. 90⁰
2. 102
3. 120
4. 100

PEMBAHASAN :
Diketahui:
∠ADC = 92⁰
∠ABC = 64
∠BAD = ∠BCD

Maka ∠BCD dapat dihitung sebagai berikut:
2.∠BCD + ∠ADC + ∠ABC = 360⁰
2.∠BCD + 92⁰ + 64⁰ = 360
2∠BCD = 360⁰ – 156⁰
∠BCD = 102
Jawaban B

Soal No.38

Perhatikan gambar di bawah ini!

Luas bangun di atas adalah … cm²

1. 1.159,5
2. 1.234,7
3. 1.115,3
4. 1.350,6

PEMBAHASAN :
Diketahui:
KQ = PQ = OQ = 9 cm
LM = 30 cm
MN = 28 cm
LO = MN = 28 cm

Penyelesaian 1:
KO = KQ + OQ = 9 cm + 9 cm = 18 cm
LP = LQ + PQ
LP = 26,5 cm + 9 cm = 35,5 cm

Maka luas layang-layang KLOP adalah:
L = ½ x LP x KO = ½ x 35,5 cm x 18 cm = 319,5 cm²

Penyelesaian 2:
L _LMNO = LM x MN = 30 cm x 28 cm = 840 cm²
Maka luas bangun KLMNOP = L _KLOP + L _LMNO
.                                                               = 319,5 cm² + 840 cm²
.                                                    =  1159,5 cm²
Jawaban B

Soal No.39

Perhatikan gambar di bawah ini!

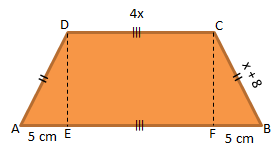
Keliling trapesium di atas adalah 82 cm. Maka nilai x adalah … cm.

1. 4,2
2. 4,8
3. 5,2
4. 5,6

PEMBAHASAN :
Diketahui:
K = 82 cm
CD = EF = 4x
AE = 5 cm
FB = 5 cm
BC = AD = x + 8
AB = AE + EF + FB

Maka keliling trapesium ABCDEF adalah:
K = 2BC + CD + AB
82 cm = 2(x+8) + 4x + (5 cm + 5 cm + 4x)
82 cm = 2x + 16 cm + 4x + 10 cm +4x
82 cm = 10x + 26 cm
56 cm = 10x
x  = 5,6 cm
Jawaban D

Soal No.40

Perhatikan gambar di bawah ini!

Luas trapesium ABCD = … cm² .

1. 65,5
2. 70
3. 79,5
4. 87

PEMBAHASAN :
Diketahui:
AB = 18 cm
BC = 8 cm
CD = 12 cm

Menentukkan tinggi trapesium:
EB = AB – DC = 18 cm – 12 cm = 6 cm

Maka luas trapesium dapat dihitung sebagai berikut:
L = ½ x (AB + DC) x AD
L = ½ x (18 cm + 12 cm) x 5,3 cm
L = ½ x 30 cm x 5,3 cm
L = 79,5 cm²
Jawaban C