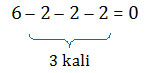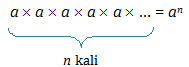pembahasan selanjutnya adalah
Tokoh Bilangan
Leonardo da Pisa adalah seorang matematikawan Italia yang berjasa dalam penulisan bilangan yang kita kenal saat ini. Ayahnya seorang perwakilan dagang di Aljazair yang mempunyai nama panggilan Bonacci. Setelah ayahnya meninggal, ia sering disebut dengan nama Fibonacci (dari kata filius Bonacci atau anak Bonacci).
 |
| Leonardo da Pisa (1175 – 1250) |
Di masa mudanya, Fibonacci berkelana ke Aljazair membantu ayahnya. Di sanalah ia tertarik dengan sistem penulisan dan penghitungan bilangan Arab. Menurutnya, sistem bilangan Arab lebih sederhana, efisien, dan lebih mudah dioperasikan daripada sistem bilangan Romawi. Akhirnya ia memutuskan untuk belajar kepada matematikawan Arab yang terkenal pada saat itu.
| Lambang Bilangan | ||||||||||
| Romawi | I | II | III | IV | V | VI | VII | VIII | IX | |
| Arab | ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ |
| Sekarang | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
Pada tahun 1202, saat usianya 27 tahun, ia pulang ke Italia dan menuliskan apa yang telah dipelajarinya dalam buku Liber Abaci atau Buku Perhitungan. Buku ini menunjukkan kepraktisan sistem penulisan bilangan Arab. Fibonacci menerapkan sistem bilangan tersebut dalam pembukuan dagang, konversi berbagai ukuran, perhitungan bunga, pertukaran uang, dan aplikasi lainnya. Ternyata buku tersebut mendapat sambutan yang baik dari kaum terpelajar Eropa. Buku tersebut menjadi inspirasi yang penting bagi pemikiran Eropa.
Pengertian Bilangan
Bilangan adalah konsep matematika yang digunakan untuk penghitungan dan pengukuran. Dalam penghitungan dan pengukuran tersebut kita membutuhkan simbol atau lambang bilangan yang disebut angka.
Jadi, angka tidak sama dengan bilangan. Angka adalah lambang bilangan. Bilangan tiga bisa dilambangkan dengan angka Romawi III, angka Arab ٣, atau angka 3.
Demikian juga, bilangan tidak sama dengan nomor. Nomor adalah urutan bilangan. Nomor tiga berarti urutan bilangan yang ketiga.
Dalam proses penghitungan dan pengukuran kita juga membutuhkan prosedur. Prosedur tersebut dinamakan operasi bilangan. Operasi bilangan yang sederhana terdiri dari operasi penjumlahan, pengurangan, perkalian, dan pembagian yang masing-masing secara berurutan dilambangkan +, −, ×, dan :.
Pengertian Bilangan Bulat
Bilangan bulat bukan berarti bilangan yang lambangnya berbentuk bulat-bulat, seperti 0, 8, 6, 9, 888, atau 6009. Bilangan 6 bukan berarti bilangan bulat berjambul atau 9 bilangan bulat berekor. Bilangan bulat adalah bilangan yang masih utuh, belum terpecah, atau belum terbagi sedikit pun.
Ibarat kue, bilangan bulat adalah sepotong kue yang masih utuh, lima potong kue yang masih utuh, atau delapan potong kue yang masih utuh. Bukan setengah potong kue, lima potong kue lebih sedikit, atau tujuh potong kue kurang sedikit.
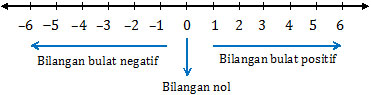
Bilangan bulat terdiri dari bilangan bulat negatif, bilangan nol, dan bilangan bulat positif.

Bilangan Nol
Bilangan nol tidak sama dengan bilangan kosong. Bilangan nol dilambangkan sedangkan bilangan kosong dilambangkan Ø (nol putul).
Bilangan nol menyatakan suatu jumlah. Artinya, karena suatu operasi bilangan, nilai bilangan menjadi nol. Ibarat tiga buah apel dalam keranjang, jika ketiga apel tersebut diambil maka jumlah apel dalam keranjang tersebut adalah nol, bukan kosong. Jika dikatakan di dalam keranjang tersebut kosong, berarti sebelumnya memang tidak pernah ada apel di dalamnya.
Bilangan nol memisahkan bilangan positif dan bilangan negatif.
Bilangan Bulat Positif
Bilangan bulat positif adalah bilangan bulat yang nilainya lebih besar daripada nol. Penulisan bilangan positif boleh diawali lambang + atau tidak. Contoh +2 (positif dua atau plus dua) atau cukup di tulis 2.
Bilangan Negatif
Bilangan negatif adalah bilangan yang nilainya kurang dari nol. Penulisan bilangan negatif wajib didahului dengan lambang −. Contoh −3 (negatif tiga, minus tiga, min tiga).
Dalam kehidupan sehari-hari bilangan bulat negatif di antaranya digunakan untuk menyatakan suhu benda atau ruang. Suhu −5 °C artinya suhu 5 °C di bawah titik beku atau di bawah 0 °C.
Bilangan nol, negatif, dan positif tersebut dapat digambarkan pada garis bilangan berikut ini.
Berdasarkan garis bilangan tersebut, bilangan bulat juga meliputi:
- Bilangan negatif : {…, −3, −2, −1}
- Bilangan nol : {0}
- Bilangan positif : {1, 2, 3, 4, …}
- Bilangan cacah : {0, 1, 2, 3, …}
- Bilangan asli : {1, 2, 3, 4, …}
- Bilangan prima : {2, 3, 5, 7, 11, …}
- Bilangan komposit : {4, 6, 8, 9, 10. ….}
Bilangan komposit adalah bilangan bulat positif lebih dari 1 yang bukan bilangan prima.
Aplikasi Bilangan Bulat
Permasalahan sehari-hari yang berhubungan dengan bilangan bulat, antara lain:
Ketinggian Tempat
Ketinggian Gunung Merapi adalah 2.968 meter sedangkan kedalaman Palung Banda adalah 7.000 meter.
Angka-angka tersebut diukur dari permukaan air laut. Bila dinotasikan ke dalam bilangan bulat, permukaan laut mewakili bilangan nol, ketinggian mewakili bilangan positif, sedangkan kedalaman mewakili bilangan negatif.
Penentuan Suhu Benda atau Suhu Ruang
Suhu udara di Eropa pada siang hari pada bulan tertentu bisa mencapai 10 °C di atas titik beku (0 °C) sedangkan pada malam hari mencapai −15 °C (15 °C di bawah titik beku).
Pembagian Wilayah menurut GMT (Greenwich Meridian Time)
Waktu Jakarta adalah GMT+7 sedangkan waktu Galapagos adalah GMT−6.
Artinya, jika di Greenwich pukul 02.00 maka di Jakarta pukul 02.00 + 7 = 09.00 sedangkan di Galapagos pukul 02.00 − 6 = −4.00. Pukul −4.00 adalah hasil penghitungan bilangan bulat, bila dikonversikan dalam sistem 24 jam akan diperoleh
24.00 – 4.00 = 20.00 atau pukul 08.00 malam.
Membandingkan Bilangan Bulat
Berdasarkan garis bilangan, bilangan bulat yang terletak sebelah kanan lebih besar daripada bilangan bulat yang terletak sebelah kiri.
Bilangan bulat positif dikatakan lebih besar apabila tersusun dari jumlah angka yang lebih banyak.
36743 > 7834
36743 lebih besar karena tersusun dari 5 angka sedangkan 7834 tersusun dari 4 angka. Ketentuan ini tidak berlaku untuk bilangan Romawi.
VIII ≯ X
Bila dua bilangan positif tersusun dari jumlah angka yang sama maka yang dibandingkan adalah angka pertama. Bila angka pertamanya sama maka dibandingkan angka kedua, ketiga, dan seterusnya.
36743 < 46743
Untuk membandingkan bilangan bulat negatif berlaku sebaliknya. Semakin besar jumlah angka penyusun bilangan bulat negatif semakin kiri letaknya dalam garis bilangan.
−36743 < −7834
−36743 > −46743
Operasi Penjumlahan dan Pengurangan Bilangan Bulat
Menjumlahkan atau mengurangkan dua bilangan yang keduanya bilangan bulat positif tidak menjadi masalah. Akan menjadi masalah jika melibatkan bilangan nol dan bilangan negatif.
Menjumlahkan dan Mengurangkan Bilangan Nol
Menjumlahkan dan mengurangkan suatu bilangan oleh bilangan nol akan menghasilkan bilangan itu sendiri.
5 + 0 = 5
5 − 0 = 5
−5 + 0 = −5
−5 – 0 = −5
Menjumlahkan suatu bilangan dari bilangan nol akan menghasilkan bilangan itu sendiri.
0 + 5 = 5
0 + (−5) = −5
Mengurangkan suatu bilangan dari bilangan nol akan menghasilkan lawan dari bilangan tersebut.
0 − 5 = −5
0 − (−5) = 5
Menjumlahkan dan Mengurangkan Bilangan Negatif
Menjumlahkan suatu bilangan dengan bilangan negatif sama dengan mengurangkan bilangan tersebut dengan bilangan positif.
5 + (−3) = 5 − 3
−5 + (−3) = −5 − 3
Mengurangkan suatu bilangan dengan bilangan negatif sama dengan menjumlahkan bilangan tersebut dengan bilangan positif.
5 − (−3) = 5 + 3
−5 − (−3) = −5 + 3
Sifat Operasi Penjumlahan dan Pengurangan Bilangan Bulat
Sifat Tertutup
Operasi penjumlahan dan pengurangan bilangan bulat bersifat tertutup, artinya operasi tersebut selalu menghasilkan bilangan bulat.
a + b = bilangan bulat
a − b = bilangan bulat
Sifat Identitas
Operasi penjumlahan dan pengurangan bilangan bulat terhadap nol bersifat identitas, artinya operasi tersebut selalu menghasilkan bilangan itu sendiri.
a + 0 = a
a − 0 = a
Sifat Komutatif
Operasi penjumlahan bilangan bulat memenuhi sifat komutatif atau pertukaran.
–5 + 3 = 3 + (–5)
Operasi pengurangan bilangan bulat tidak memenuhi sifat komutatif.
–5 – 3 ≠ 3 – (–5)
Sifat Asosiatif
Operasi penjumlahan bilangan bulat memenuhi sifat asosiatif atau pengelompokan.
(–5 + 3) + 4 = –5 + (3 + 4)
Intermezzo
Penjumlahan bilangan 1 sampai dengan 9 yang mempunyai inisial sama selalu menghasilkan 10.
Operasi Perkalian dan Pembagian Bilangan Bulat
Hubungan Perkalian dan Penjumlah
Perkalian adalah penjumlahan berulang terhadap bilangan yang sama.
3 × 4 = 4 + 4 + 4
Bukan 3 + 3 + 3 + 3
3 × 4 artinya bilangan 4 dijumlahkan sebanyak 3 kali, bukan bilangan 3 dijumlahkan sebanyak 4 kali, meskipun hasilnya sama.
Perhatikan contoh lain berikut ini!
3 × ayam = ayam + ayam + ayam = 3 ayam
3 × a = a + a + a = 3a
Keadaan sebaliknya sulit dinalar.
Hubungan Pembagian dengan Pengurangan
Pembagian adalah pengurangan berulang terhadap bilangan yang sama.
6 : 2 berarti pengurangan bilangan 6 oleh bilangan 2 sebanyak n kali sampai habis (menghasilkan nol).
Jadi 6 : 2 = 3
Perkalian Bilangan Bulat Positif dan Negatif
Perhatikan tabel berikut ini!
| × | + | − |
| + | + | − |
| − | − | + |
Hasil perkalian atau pembagian dua bilangan bulat bertanda sama adalah bilangan bulat positif.
3 × 5 = 15
−3 × (−5) = 15
15 : 3 = 5
(−15) : (−3) = 5
Hasil perkalian atau pembagian dua bilangan bulat berbeda tanda adalah bilangan bulat negatif.
3 × (−5) = −15
−3 × 5 = −15
15 : (−3) = −5
(−15) : 3 = −5
Perkalian dengan Bilangan Nol
Hasil perkalian bilangan bulat positif atau negatif dengan nol adalah nol.
5 × 0 = 0
0 × 5 = 0
−5 × 0 = 0
0 × (−5) = 0
Hasil pembagian bilangan nol dengan bilangan positif atau negatif adalah nol.
0 : 5 = 0
0 : (−5) = 0
Hasil Pembagian bilangan bulat positif atau negatif dengan nol adalah tidak terdefinisikan.
5 : 0 = E (error atau tidak terdefinisikan)
−5 : 0 = E (error atau tidak terdefinisikan)
Banyak yang menyangka 5 : 0 hasilnya 0. Coba perhatikan ilustrasi berikut ini!
8 : 2 = 4 karena 4 × 2 = 8
: 5 = karena × 5 =
5 : = karena × = 5 ??????
Sifat Operasi Perkalian dan Pembagian Bilangan Bulat
Sifat Tertutup
Operasi perkalian bilangan bulat bersifat tertutup.
a × b = bilangan bulat
Operasi pembagian bilangan bulat bersifat tidak tertutup.
a : b = belum tentu bilangan bulat
Sifat Identitas
Operasi perkalian dan pembagian terhadap bilangan satu bersifat identitas.
a × 1 = a
a : 1 = a
Sifat Komutatif
Operasi perkalian bilangan bulat memenuhi sifat komutatif atau pertukaran.
–5 × 3 = 3 × (–5)
Operasi pembagian tidak memenuhi sifat komutatif.
–5 : 3 ≠ 3 : (–5)
Sifat Asosiatif
Operasi perkalian bilangan bulat memenuhi sifat asosiatif atau pengelompokan.
(–5 × 3) × 4 = –5 × (3 × 4)
Perpangkatan Bilangan Bulat
Perpangkatan adalah perkalian berulang terhadap bilangan yang sama.
a disebut bilangan basis atau bilangan pokok sedangkan n disebut bilangan pangkat.
an dibaca a pangkat n
Sifat Perpangkatan Bilangan Bulat
Bilangan bulat positif pangkat bilangan genap atau bilangan ganjil menghasilkan bilangan bulat positif.
24 = 2 × 2 × 2 × 2 = 16
25 = 2 × 2 × 2 × 2 × 2 = 32
Bilangan bulat negatif pangkat bilangan genap menghasilkan bilangan bulat positif, sedangkan pangkat ganjil menghasilkan bilangan negatif.
(−2)4 = (−2) × (−2) × (−2) × (−2) = 16
(−2)3 = (−2) × (−2) × (−2) = −8
Hati-hati!
(−2)4 ≠ −(2)4
(−2)4 = −2 × (−2) × (−2) × (−2) = 16
−(2)4 = − (2) × (2) ×(2) ×(2) = −16
Bilangan bulat pangkat negatif dibahas di kelas 9.
Materi berikutnya, Bilangan Pecahan.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat