Baiklah teman teman selanjutnya kita akan menyelesaikan soal di bawah ini
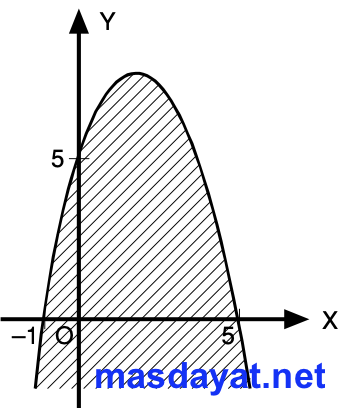
Daerah penyelesaian dari pertidaksamaan y ≤ -x2 + 4x + 5 adalah
Pembahasan:
Untuk Pertidaksamaan y≤x²+4x−5., kita gambar terlebih kurva y = x²+4x−5, sebagai berikut:
Titik potong sumbu x, y = 0.
0 = x²+4x−5
(x+5)(x-1) = 0
x+5 = 0
x = -5
atau
x-1 = 0
x = 1
Jadi koordinat titik potong sumbu x kurva y = x²+4x−5 adalah (-5, 0) dan (1, 0).
Titik potong sumbu y, x = 0.
y = 0²+4(0)−5
y = -5
Jadi koordinat titik potong sumbu y kurva y = x²+4x−5 adalah (0, -5).
Koordinat titik puncak:
(xp, yp) = (-b/2a, -D/4a)
(xp, yp) = (-4/2(1), -(4²-4(1)(-5))/4(1))
(xp, yp) = (-4/2, -36/4)
(xp, yp) = (-2, -9)
Untuk menentukan daerah pertidaksamaan, maka uji titik (0,0) sehingga diperoleh 0 ≤ -5 , pernyataan salah, sehingga titik (0,0) bukan pada daerah penyelesaian. sehingga daerah penyelesaian berada di luar kurva.
Dari uraian di atas, maka daerah penyelesaian pertidaksamaan dapat digambarkan sebagai berikut: (Perhatikan gambar dan daerah yag berwarna abu-abu)
Kesimpulan:
Jadi daerah penyelesaian dari pertidaksamaan y≤x²+4x−5 adalah daerah yang berwarna abu-abu seperti pada gambar.