pembahasan selanjutnya adalah
- persamaan kuadrat baru,
- jenis akar persamaan kuadrat,
- persamaan linear,
- persamaan lingkaran, dan
- garis singgung lingkaran.
Soal No. 6 tentang Akar Persamaan Kuadrat Baru
A. x2 + 2x − 13 = 0
B. x2 + 2x + 13 = 0
C. x2 − 2x − 13 = 0
D. x2 + 2x − 21 = 0
E. x2 − 2x − 21 = 0
Pembahasan
Cara 1
Persamaan kuadrat x2 + 6x − 5 = 0 akar-akarnya α dan β, diperoleh
α + β = −b/a = −6
α . β = c/a = −5
Persamaan kuadrat baru yang akar-akarnya (α + 2) dan (β +2) adalah
x2 − px + q = 0
dengan p = (α + 2) + (β +2) dan q = (α + 2) . (β +2)
Mari kita tentukan nilai p dan q.
p = (α + 2) + (β +2)
= (α + β) + 4
= −6 + 4
= −2
q = (α + 2) . (β +2)
= αβ + 2α + 2β + 4
= αβ + 2(α + β) + 4
= −5 + 2.(−6) + 4
= −13
Dengan demikian persamaan kuadra baru tersebut adalah
x2 − px + q = 0
x2 + 2x − 13 = 0
Cara 2
Akar-akar persamaan kuadrat lama: α dan β
Akar-akar persamaan kuadrat baru : (α + 2) dan (β + 2)
Misal x = α + 2
maka α = x − 2
Persamaan kuadrat lama: x2 + 6x − 5 = 0
Persamaan kuadrat baru : α2 + 6α − 5 = 0
Substitusi α = x − 2 pada persamaan kuadrat baru:
α2 + 6α − 5 = 0
(x − 2)2 + 6(x − 2) − 5 = 0
x2 − 4x + 4 + 6x − 12 − 5 = 0
x2 + 2x − 13 = 0
Jadi, persamaan kuadrat baru dari persamaan kuadrat tersebut adalah x2 + 2x − 13 = 0 (A).
Perdalam materi ini di Pembahasan Matematika IPA UN: Persamaan dan Fungsi Kuadrat.
Soal No. 7 tentang Jenis Akar Persamaan Kuadrat
A. m > 10/3 atau m < 1
B. m ≥ 10/3 atau m ≤ −1
C. m ≥ 1 atau m ≤ −10/3
D. m > 10/3 atau m < −1
E. m > 1 atau m < −10/3

Pembahasan
Dari persamaan kuadrat (m − 5)x2 − 4mx + m − 2 = 0 diperoleh data:
a = m − 5,
b = −4m,
c = m − 2.
Syarat agar persamaan kuadrat tersebut mempunyai akar real adalah
D ≥ 0
b2 − 4ac ≥ 0
(−4m)2 − 4(m − 5)(m − 2) ≥ 0
16m2 − 4(m2 − 7m + 10) ≥ 0
12m2 + 28m − 40) ≥ 0
3m2 + 7m − 10) ≥ 0
(3m + 10) (m − 1) ≥ 0
Sekarang tinggal membuat garis bilangannya.

Berdasarkan garis bilangan pertidaksamaan tersebut diperoleh
m ≥ 1 atau m ≤ −10/3
Jadi, batas-batas nilai m agar persamaan kuadrat tersebut mempunyai dua akar real adalah opsi (C).
Soal No. 8 tentang Persamaan Linear
A. Rp49.500,00
B. Rp47.500,00
C. Rp35.000,00
D. Rp32.500,00
E. Rp29.500,00
Pembahasan
Kita misalkan terlebih dahulu.
x : jeruk
y : mangga
z : jambu
Selanjutnya kita buat persamaan matematikanya.
Malik : 2x + 1½y + z = 72.000 … (1)
Aziz : 3x + ½y + ½z = 61.000 … (2)
Sulasmini : x + 2y + 2z = 79.000 … (3)
Ani : ½x + 1½y + z = ?
Perhatikan persamaan (2) dan (3). Koefisien y dan z pada kedua persamaan tersebut mempunyai perbandingan yang sama. Jadi dengan mengeliminasi kedua persamaan tersebut, dua variabel akan langsung tereliminasi.
Mari kita eliminasi. Persamaan (2) kita kalikan 4 sedangkan persamaan (3) kita biarkan apa adanya.
12x + 2y + 2z = 244.000
x + 2y + 2z = 79.000
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ −
11x = 165.000
x = 15.000
Sekarang perhatikan persamaan matematika dari Malik dan Ani. Kedua persamaan tersebut mempunyai koefisien y dan z yang sama bukan? Berarti kita cukup melakukan substitusi x = 15.000 ke persamaan (1).
2 × 15.000 + 1½y + z = 72.000
1½y + z = 42.000
Sekarang kita sudah dapat menentukan harga yang harus dibayar oleh Ani.
½x + 1½y + z
= ½ × 15.000 + 42.000
= 7.500 + 42.000
= 49.500
Jadi, Ani harus membayar buah-buahan yang dibelinya sebesar Rp49.500,00 (A).
Perdalam materi ini di Pembahasan Matematika UN: Sistem Persamaan dan Pertidaksamaan Linear.
Soal No. 9 tentang Persamaan Lingkaran
A. x2 + y2 + 2x + 4y − 27 = 0
B. x2 + y2 + 2x − 4y − 27 = 0
C. x2 + y2 + 2x − 4y − 32 = 0
D. x2 + y2 − 4x − 2y − 32 = 0
E. x2 + y2 − 4x + 2y − 7 = 0
Pembahasan
Perhatikan gambar di bawah ini!
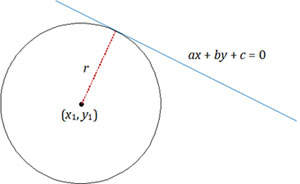
Jarak tegak lurus titik pusat ke garis tersebut merupakan jari-jari lingkaran. Rumus jarak titik ke garis adalah
Persamaan lingkaran tersebut adalah
(x − x1)2 + (y − y1)2 = r2
(x + 1)2 + (y − 2)2 = (4√2)2
x2 + 2x + 1 + y2 − 4y + 4 = 32
x2 + y2 + 2x − 4y − 27 = 0
Jadi, persamaan lingkaran tersebut adalah opsi (B).
Perdalam materi ini di Pembahasan Matematika IPA UN: Lingkaran.
Soal No. 10 tentang Garis Singgung Lingkaran
A. y = 2x − 14
B. y = 2x − 11
C. y = 2x + 5
D. y = 2x + 9
E. y = 2x + 15
Pembahasan
Persamaan lingkaran x2 + y2 + 2x − 6y − 10 = 0 mempunyai bentuk umum
x2 + y2 + 2Ax + 2By + C = 0
Berdasarkan bentuk umum tersebut diperoleh
2A = 2
A = 1
2B = −6
B = −3
C = −10
Pusat dan jari-jari lingkaran tersebut adalah
pusat (−A, −B)
pusat (−1, 3) → (h, k)
Misal gradien garis x + 2y + 1 = 0 adalah m1, maka
m1 = −a/b
= −1/2
Garis singgung lingkaran tegak lurus dengan garis tersebut sehingga perkalian gradien garis (m1) dengan gradien garis singgung lingkaran (m2) sama dengan −1.
m1 . m2 = −1
−½ . m2 = −1
m2 = 2
Persamaan garis singgung lingkaran yang berpusat (h, k), jari-jari r, dan gradien m2 adalah
y − 3 = 2x + 2 ± 10
y = 2x + 5 ± 10
y = 2x + 15 dan y = 2x − 5
Jadi, salah satu persamaan garis singgung lingkaran tersebut adalah y = 2x + 15 (E).
Perdalam materi ini di Pembahasan Matematika IPA UN: Lingkaran.
Simak Pembahasan Soal Matematika IPA UN 2015 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
