pembahasan selanjutnya adalah
- operasi vektor,
- sudut antara dua vektor,
- proyeksi vektor,
- transformasi geometri, dan
- pertidaksamaan logaritma.
Soal No. 16 tentang Operasi Vektor
A. 5i + 8j + 6k
B. 5i + 8j − 6k
C. 5i − 8j + 6k
D. 6i + 5j − 8k
E. 6i − 5j + 6k
Pembahasan
Notasi vektor dalam bentuk kombinasi linear i, j, k, terkesan lebih sulit. Karena itu ubahlah ke bentuk kolom atau baris.
a = (4, 2, −5)
b = (1, 3, x)
c = (6, 5, 2)
Bentuk di atas tampak lebih ramah. Meski tidak memengaruhi kecepatan mengerjakan, setidaknya dapat menambah semangat dan energi. Ok, lanjut!
Jika dua vektor saling tegak lurus maka perkalian dot-nya sama dengan nol.
a . b = 0
4 . 1 + 2 . 3 + (−5) . x = 0
10 − 5x = 0
5x = 10
x = 2
Substitusikan x = 2 pada vektor b sehingga diperoleh b = (1, 3, 2). Selanjutnya tinggal menyelesaikan tahap akhir.
2a + 3b − c
Jadi, hasil dari 2a + 3b − c = 5i + 8j − 6k (B).
Perdalam materi ini di Pembahasan Matematika IPA UN: Operasi Vektor.
Soal No. 17 tentang Sudut antara Dua Vektor
A. 1
B. ⅘
C. 0
D. −½
E. −1

Pembahasan
Modal utama untuk menyelesaikan soal ini adalah mengetahui bahwa berlaku rumus
|a + b|2 = |a|2
25 = 16 + 9 + 2ab cos θ
2ab cos θ = 0
cos θ = 0
θ = 90°
cos 2θ = cos 180°
= −1
Jadi, nilai dari cos 2θ = −1 (E).
Perdalam materi ini di Pembahasan Matematika IPA UN: Sudut antara Dua Vektor.
Soal No. 18 tentang Proyeksi Vektor
A. −4
B. −2
C. 2
D. 4
E. 8
Pembahasan
Untuk menyelesaikan soal proyeksi skalar, kita perlu menentukan perkalian vektor a dan b serta menentukan panjang vektor b.
a = (2, −p, 3)
b = (1, −2, 2)
a . b = 2 + 2p + 6
= 8 + 2p
= 3
Proyeksi skalar vektor a terhadap b dirumuskan
12 = 8 + 2p
2p = 4
p = 2
Jadi, nilai p adalah 2 (C).
Perdalam materi ini di Pembahasan Matematika IPA UN: Proyeksi Vektor.
Soal No. 19 tentang Transformasi Geometri
A. 2x + 5y − 3 = 0
B. 2x − 5y − 3 = 0
C. 2x + 5y + 3 = 0
D. 5x − 2y − 3 = 0
E. 5x − 2y + 3 = 0
Pembahasan
T1 adalah transformasi pencerminan terhadap garis y = x.
T1 : P(x, y) —→ P’(y, x)
T2 adalah rotasi dengan pusat O(0, 0) sebesar 90° dengan arah putar berlawanan dengan putaran jarum jam.
T adalah transformasi T1 dilanjutkan T2.
T = T2 o T1
Berdasarkan matriks komposisi tersebut diperoleh
x‘ = −x → x = −x‘
y‘ = y → y = y‘
Dengan demikian bayangan garis 2x − 5y + 3 = 0 adalah
2x − 5y + 3 = 0
2(−x’) − 5y’ + 3 = 0
−2x‘ − 5y’ + 3 = 0
2x’ + 5y’ − 3 = 0
Jadi, persamaan bayangan garis tersebut adalah 2x + 5y − 3 = 0 (A).
Perdalam materi ini di Pembahasan Matematika IPA UN: Transformasi Geometri.
Soal No. 20 tentang Pertidaksamaan Logaritma
A. 4/3 < x < 8 atau x < −2
B. 0 < x < 8 atau x < −2
C. 0 < x < 8 atau −2 < x < −1/3
D. x > 8 atau x < −2
E. x > 8 atau −2 < x < −1/3
Pembahasan
Yang perlu diperhatikan pertama kali saat mengerjakan soal pertidaksamaan logaritma adalah syarat yang berlaku bagi fungsi logaritma tersebut. Syarat ini sebaiknya dikerjakan terlebih dahulu agar tidak kelupaan.
Bilangan atau fungsi yang di-log syaratnya harus bernilai positif.
3x2 + x > 0
x(3x + 1) > 0
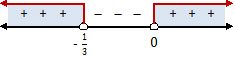
8 − x > 0
−x > −8
x

Hal kedua yang perlu diperhatikan adalah bilangan pokok logaritma. Karena bilangan pokoknya 3 (lebih dari 1), penyelesaiannya tidak merubah tanda pertidaksamaan.
3log (3x2 + x) < 3log (8 − x)
3x2 + x < 8 − x
3x2 + 2x − 8 < 0
(3x − 4)(x + 2) < 0

Gabungan dari ketiga garis bilangan tersebut merupakan penyelesaian akhir pertidaksamaan logaritma di atas.

Jadi, penyelesaian pertidaksamaan tersebut adalah 0 xx
Perdalam materi ini di Pembahasan Matematika UN: Pertidaksamaan Eksponen dan Logaritma.
Simak Pembahasan Soal Matematika IPA UN 2015 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat