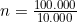pembahasan selanjutnya adalah
- aritmetika sosial,
- barisan aritmetika,
- deret geometri,
- deret aritmetika, dan
- bentuk aljabar.
Soal No. 6 tentang Aritmetika Sosial
A. 8 bulan
B. 10 bulan
C. 12 bulan
D. 15 bulan
Pembahasan
Bunga tabungan Aldi selama setahun:
15% × Rp800.000,00
= Rp120.000,00
Bunga tabungan Aldi selama sebulan:
Rp120.000,00 : 12
= Rp10.0000,00
Saat diambil, uang tabungan Aldi menjadi Rp900.000,00, berarti bunganya adalah:
Rp900.000,00 − Rp800.000,00
= Rp100.000,00
Dengan bunga sebesar itu, berarti Aldi telah menabung selama:
= 10
Jadi, lama Aldi menabung adalah 10 bulan (B).
Soal No. 7 tentang Barisan Aritmetika
A. 181
B. 176
C. 124
D. 20

Pembahasan
Dari barisan tersebut diketahui:
suku awal : a = 6
beda : b = 5
Suku ke-n deret aritmetika dapat ditentukan dengan rumus:
Un = a + (n − 1)b
U35 = 6 + (35 − 1)×5
= 6 + 34 × 5
= 6 + 170
= 176
Jadi, suku ke-35 barisan aritmetika tersebut adalah 176 (B).
Soal No. 8 tentang Deret Geometri
A. 140 m
B. 132 m
C. 128 m
D. 124 m
Pembahasan
Data yang dapat diperoleh dari soal:
n = 5
a = 4
U5 = 64
Kita manfaatkan data U5 = 64 untuk mendapatkan nilai rasio r.
Un = arn−1
U5 = ar4
64 = 4r4
r4 = 16
r4 = 24
r = 2
Panjang tali semula merupakan jumlah kelima potongan tali tersebut atau U5.
= 4 × (32 − 1)
= 4 × 31
= 124
Jadi, panjang tali semula adalah 124 m (D).
Soal No. 9 tentang Deret Aritmetika
A. 11.700
B. 12.700
C. 15.161
D. 14.121
Pembahasan
Jumlah bilangan kelipatan 5 antara 200 dan 400 membentuk deret aritmetika sebagai berikut:
205 + 210 + 215 + … + 395
Dari deret aritmetika tersebut diperoleh:
a = 205
b = 5
Un = 395
Kita manfaatkan data Un = 395 untuk mendapatkan nilai n.
Un = 395
a + (n − 1)b = 395
205 + (n − 1)×5 = 395
5(n − 1) = 190
n − 1 = 38
n = 39
Selanjutnya, kita tinggal memasukkan data-data tersebut pada rumus jumlah.
Sn = 1/2 n (a + Un)
S39 = 1/2 × 39 × (205 + 395)
= 1/2 × 39 × 600
= 11.700
Jadi, jumlah bilangan kelipatan 5 antara 200 dan 400 adalah 11.700 (A).
Soal No. 10 tentang Bentuk Aljabar
I. 4x2 − 9 = (2x + 3)(2x − 3)
II. 2x2 + x − 3 = (2x − 3)(x + 1)
III. x2 + x − 6 = (x + 3)(x − 2)
IV. x2 + 4x − 5 = (x − 5)(x + 1)
Pernyataan yang benar adalah ….
A. I dan II
B. II dan III
C. I dan III
D. II dan IV
Pembahasan
Mari kita periksa satu per satu!
I. 4x2 − 9 = (2x)2 − 32
= (2x + 3)(2x − 3)
[pernyataan I benar]
II. 2x2 + x − 3 = (2x + 3)(x − 1)
[pernyataan II salah]
III. x2 + x − 6 = (x + 3)(x − 2)
[pernyataan III benar]
IV. x2 + 4x − 5 = (x + 5)(x − 1)
[pernyataan IV salah]
Jadi, pernyataan yang benar adalah pernyataan I dan III (C).
Simak Pembahasan Soal Matematika SMP UN 2015 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat