pembahasan selanjutnya adalah
- unsur-unsur bangun ruang,
- kerangka bangun ruang,
- volume bangun ruang, dan
- luas permukaan bangun ruang.
Soal No. 31 tentang Unsur-unsur Bangun Ruang
A. 4
B. 6
C. 8
D. 12
Pembahasan
Untuk menentukan jumlah diagonal suatu balok, sebaiknya kita gambar bangun balok terlebih dahulu.
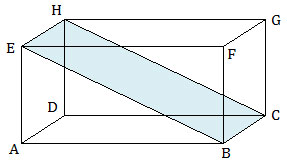
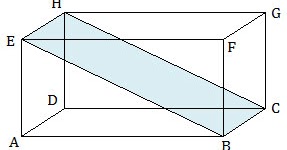
Pada gambar di atas, BCHE adalah bidang diagonal balok. Seluruh bidang diagonal balok tersebut adalah:
- BCHE
- ADGF
- ABGH
- CDEF
- AEGC
- BFHD
Jadi, banyak bidang diagonal balok adalah 6 buah (B).
Soal No. 32 tentang Kerangka Bangun Ruang
A. 7 buah
B. 8 buah
C. 9 buah
D. 10 buah

Pembahasan
Perhatikan kerangka limas persegi berikut ini!
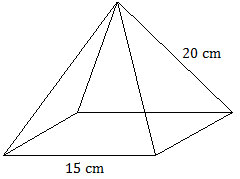
Limas persegi mempunyai 4 rusuk alas yang sama panjang dan 4 rusuk tegak yang sama panjang sehingga panjang seluruh rusuk yang diperlukan untuk membuat satu limas persegi adalah:
panjang seluruh rusuk = 4 × rusuk alas + 4 × sisi tegak
= 4 × 15 cm + 4 × 20 cm
= 60 cm + 80 cm
= 140 cm
Jika tersedia kawat 10 m (=1000 cm) maka dapat dibuat kerangka limas sebanyak:
banyak limas = 1000 : 140
= 7,14
Jadi, kerangka limas yang dapat dibuat adalah 7 buah (A).
Soal No. 33 tentang Volume Bangun Ruang (Belahan Bola)
A. 1.024π cm3
B. 1.152π cm3
C. 1.296π cm3
D. 2.304π cm3
Pembahasan
Diameter bola 24 cm berarti jari-jari bola 12 cm.
Volume belahan bola adalah setengah dari volume bola.
V = 1/2 × volume bola
= 1/2 × 4/3 πr3
= 2/3 × πr3
= 2/3 × π × 123
= 2/3 × π × 1728
= 1.152π
Jadi, volume belahan bola tersebut adalah 1.152π cm3 (B).
Soal No. 34 tentang Volume Bangun Ruang (Kerucut)
A. 2.310 cm3
B. 3.140 cm3
C. 4.620 cm3
D. 4.710 cm3
Pembahasan
Volume kerucut tersebut adalah:
(angka berwarna merah bisa dicoret)
= 22 × 21 × 10
= 4.620
Jadi, volume kerucut tersebut adalah 4.620 cm3 (C).
Soal No. 35 tentang Luas Permukaan Bangun Ruang
A. 536 cm2
B. 596 cm2
C. 616 cm2
D. 656 cm2
Pembahasan
Data-data yang diketahui pada soal:
d1 = 10 cm
d2 = 24 cm
t = 8 cm
Perhatikan prisma belah ketupat berikut ini!

Sisi alas prisma (s) dapat ditentukan dengan teorema Pythagoras.
= 13
Prisma tersebut mempunyai 2 sisi yang luasnya sama, yaitu sisi alas dan sisi atas. serta 4 sisi tegak yang luasnya sama. Dengan demikian, luas permukaan prisma adalah jumlah dari 2 kali luas alas dan 4 kali luas sisi tegak.
L = 2La + 4Lst
= 2 (½ × d1 × d2) + 4 (s × t)
= 2 (½ × 10 × 24) + 4 (13 × 8)
= 240 + 416
= 656
Jadi, luas permukaan prisma belah ketupat tersebut adalah 656 cm2 (D).
Simak Pembahasan Soal Matematika SMP UN 2015 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat