pembahasan selanjutnya adalah
- luas permukaan bangun ruang,
- ukuran pemusatan (modus),
- ukuran pemusatan (rata-rata),
- penyajian dan penafsiran data, serta
- peluang kejadian.
Soal No. 36 tentang Luas Permukaan Bangun Ruang
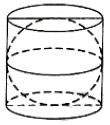
Jika luas permukaan bola 90 cm2, luas seluruh permukaan tabung adalah ….
A. 160 cm2
B. 150 cm2
C. 135 cm2
D. 120 cm2
Pembahasan
Luas permukaan bola (Lb) sama dengan 90 cm2.
Lb = 4πr2
90 = 4πr2
πr2 = 90 : 4
πr2 = 22,5
Pada gambar di atas, selimut tabung tepat bersentuhan dengan kulit bola, berarti jari-jari tabung sama dengan jari-jari bola. Selain itu, alas dan atap tabung juga tepat bersentuhan dengan kulit bola sehingga tinggi tabung sama dengan diameter bola.
t = d
t = 2r
Luas seluruh permukaan tabung (Lt) adalah jumlah dari 2 kali luas alas (La) dengan luas selimut (Ls).
Lt = 2La + Ls
Lt = 2πr2 + 2πrt
= 2πr2 + 2πr.2r (substitusi t = 2r)
= 2πr2 + 4πr2
= 6πr2
= 6 × 22,5 (substitusi πr2 = 22,5)
= 135
Jadi, luas seluruh permukaan tabung pada gambar di atas adalah 135 cm2 (C).
Soal No. 37 tentang Ukuran Pemusatan (Modus)
30, 35, 45, 35, 25, 25, 40, 35, 40.
Pertanyaan yang benar adalah ….
A. modus = 25, yaitu data terkecil
B. modus = 25, yaitu data yang letaknya di tengah-tengah
C. modus = 35, yaitu data yang terletak di tengah setelah data diurutkan
D. modus = 35, yaitu data yang mempunyai frekuensi terbanyak

Pembahasan
Modus adalah nilai yang sering muncul atau nilai dengan frekuensi terbanyak. Pada data di atas, nilai 35 muncul tiga kali dan paling banyak di antara nilai-nilai yang lain, sehingga modus data di atas adalah 35.
Jadi, pernyataan yang benar adalah opsi (D).
Soal No. 38 tentang Ukuran Pemusatan (Rata-rata)
A. 114,6
B. 115
C. 116
D. 116,4
Pembahasan
Misal data untuk siswa laki-laki berindeks (1) dan data untuk siswa perempuan berindeks (2).
n1 = 12
x1 = 110
n2 = 18
x2 = 120
Rata-rata gabungan siswa laki-laki dan perempuan adalah:
(nol bisa dicoret, angka hijau dibagi 3)
= 4×11 + 6×12
= 44
Jadi, Rata-rata hasil tes IQ seluruh siswa dalam kelas tersebut adalah 116 (C).
Soal No. 39 tentang Penyajian dan Penafsiran Data
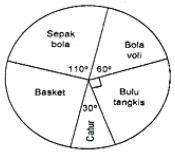
Jika banyak siswa yang gemar catur 15 orang, banyak siswa yang gemar basket adalah ….
A. 35 orang
B. 45 orang
C. 55 orang
D. 70 orang
Pembahasan
Langkah pertama adalah menentukan sudut diagram untuk siswa yang gemar basket (∠B).
∠B = 360° − (30 + 90 + 60 + 110)°
= 360° − 290°
= 70°
Untuk menentukan banyak siswa yang gemar basket, kita banding dengan siswa yang gemar catur (C).
= 7/3 × 15
= 35
Jadi, banyak siswa yang gemar basket adalah 35 orang (A).
Soal No. 40 tentang Peluang Kejadian
A. 0,03
B. 0,15
C. 0,25
D. 0,30
Pembahasan
Ruang sampel soal di atas adalah jumlah pengunjung pameran bibit unggul.
n(S) = 300
Jika A adalah kejadian dibagikannya bibit unggul maka:
n(A) = 75
Peluang kejadian A adalah:
= 75/300
= 0,25
Jadi, peluang setiap pengunjung untuk mendapatkan bibit tersebut adalah 0,25 (C).
Simak Pembahasan Soal Matematika SMP UN 2015 selengkapnya.
Simak juga:
Pembahasan Matematika SMP UN 2014
Pembahasan Matematika SMP UN 2016
Pembahasan Matematika SMP UN 2017
Pembahasan Matematika SMP UN 2018
Pembahasan Matematika SMP UN 2019
Pembahasan Matematika SMP UN 2019 (2)
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
