pembahasan selanjutnya adalah
- peluang kejadian,
- statistika (ukuran pemusatan),
- statistika (ukuran letak),
- kaidah pencacahan dan permutasi, serta
- kombinasi.
Soal No. 36 tentang Peluang Kejadian
A. 1/66
B. 1/33
C. 3/22
D. 1/6
E. 2/11
Pembahasan
Di toko tersebut terdapat 12 lampu: 2 lampu rusak dan 10 lampu masih baik. Peluang pembeli ketiga mendapatkan lampu rusak bergantung pada pembeli pertama dan kedua. Ada 3 kemungkinan pembeli ketiga mendapatkan lampu rusak.
P1 : Pembeli I mendapatkan lampu baik, pembeli II mendapatkan lampu baik, dan pembeli III mendapatkan lampu rusak.
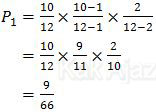
Artinya, saat pembeli I membeli, jumlah lampu masih 12 dan yang masih dalam keadaan baik ada 10. Ketika pembeli II membeli, jumlah lampu tinggal 11 dan yang baik tinggal 9. Ketika pembeli ketiga membeli, jumlah lampu tinggal 9 dan yang rusak masih 2 karena pembeli I dan II mendapatkan lampu baik.
Ok, lanjut!
P2 : Pembeli I mendapatkan lampu baik, pembeli II mendapatkan lampu rusak, dan pembeli III mendapatkan lampu rusak.

P3 : Pembeli I mendapatkan lampu rusak, pembeli II mendapatkan lampu baik, dan pembeli III mendapatkan lampu rusak.

Dengan demikian, peluang pembeli ketiga mendapatkan lampu rusak adalah peluang P1, P2, atau P3.
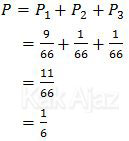
Jadi, peluang pembeli ketiga mendapatkan lampu rusak adalah 1/6 (D).
Perdalam materi ini di Pembahasan Matematika IPA UN: Teori Peluang.
Soal No. 37 tentang Statistika (ukuran pemusatan)
A. 47,5
B. 46,5
C. 46,4
D. 45,2
E. 44,7

Pembahasan
Untuk menentukan modus digunakan rumus:
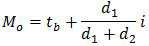
Perhatikan penentuan besaran-besaran modus berikut ini!
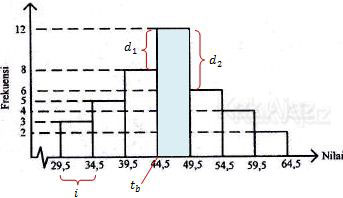
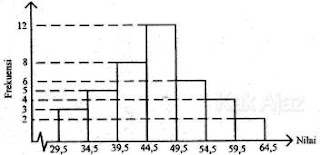
Bagian yang diarsir biru adalah kelas modus. Berdasarkan histogram di atas, diperoleh:
tb = 44,5
d1 = 12 − 8
= 4
d2 = 12 − 6
= 6
i = 34,5 − 29,5
= 5
Dengan demikian, modus data tersebut adalah:
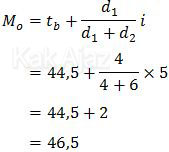
Jadi, modus dari data yang disajikan dalam histogram di atas adalah 46,5 (B).
Perdalam materi ini di Pembahasan Matematika IPA UN: Statistika.
Soal No. 38 tentang Statistika (Ukuran Letak)
| Nilai | Frekuensi |
| 31 − 40 | 3 |
| 41 − 50 | 5 |
| 51 − 60 | 10 |
| 61 − 70 | 11 |
| 71 − 80 | 8 |
| 81 − 90 | 3 |
Kuartil bawah dari data pada tabel tersebut adalah ….
A. 48,5
B. 51,5
C. 52,5
D. 54,5
E. 58,5
Pembahasan
Kuartil bawah atau disebut juga Q1 dirumuskan sebagai:
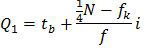
Perhatikan penentuan besaran-besaran kuartil bawah berikut ini!
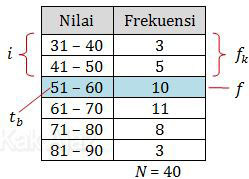
Kuartil bawah terletak pada data ke ¼N (data yang berarsir biru). Berdasarkan tabel di atas diperoleh:
tb = 51 − 0,5
= 50,5
f = 10
fk = 3 + 5
= 8
i = 41 − 31
= 10
Dengan demikian, kuartil bawah data tersebut adalah:
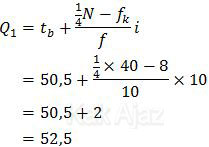
Jadi, kuartil bawah dari data pada tabel tersebut adalah 52,5 (C).
Perdalam materi ini di Pembahasan Matematika IPA UN: Statistika.
Soal No. 39 tentang Kaidah Pencacahan dan Permutasi
A. 120
B. 180
C. 240
D. 360
E. 720
Pembahasan
Cara I: Permutasi
Bilangan 4 angka yang disusun dari 6 angka adalah:
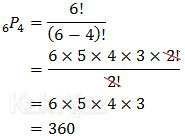
Bilangan 4 angka yang lebih dari 4.000 tentu saja bilangan yang berkepala 4, 5, 6, dan 7 (ada 4 angka). Sedangkan seluruh angka yang disusun terdiri dari 6 angka. Sehingga banyak bilangan yang lebih dari 4.000 adalah:
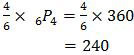
Cara II: Kaidah Pencacahan
Perhatikan susunan bilangan 4 angka berikut ini!
ribuan:
Karena harus lebih dari 4.000 maka angka yang harus mengisi posisinya adalah 4, 5, 6, dan 7 (ada 4 angka)
ratusan:
Semua angka boleh mengisi posisi ini, tetapi karena 1 angka telah menempati posisi ribuan maka banyak angka yang menempati posisi ratusan ada 5 angka (6 − 1).
puluhan:
Semua angka boleh mengisi posisi ini, tetapi karena 2 angka telah menempati posisi ribuan dan ratusan maka banyak angka yang menempati posisi puluhan ada 4 angka (6 − 2).
satuan:
Semua angka boleh mengisi posisi ini, tetapi karena 3 angka telah menempati posisi ribuan, ratusan, dan puluhan maka banyak angka yang menempati posisi satuan ada 3 angka (6 − 3).
Dengan demikian, banyak bilangan 4 angka tersebut adalah:
4 × 5 × 4 × 3 = 240
Jadi, banyak bilangan yang lebih dari 4.000 adalah 240 (C).
Perdalam materi ini di Pembahasan Matematika IPA UN: Kaidah Pencacahan, Permutasi, dan Kombinasi.
Soal No. 40 tentang Kombinasi
A. 21
B. 28
C. 45
D. 48
E. 56
Pembahasan
Dari 10 soal wajib dikerjakan 8 soal. 3 soal sudah pasti dikerjakan (nomor 1, 3, dan 5). Sehingga sisa soal tinggal 7 dan soal yang harus dikerjakan tinggal 5.
Banyak cara memilih soal adalah:
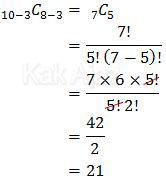
Jadi, banyak cara peserta ujian memilih soal yang dikerjakan adalah 21 cara (A).
Perdalam materi ini di Pembahasan Matematika IPA UN: Kaidah Pencacahan, Permutasi, dan Kombinasi.
Simak Pembahasan Soal Matematika IPA UN 2016 selengkapnya.
Simak juga:
Pembahasan Matematika IPA UN 2013
Pembahasan Matematika IPA UN 2014
Pembahasan Matematika IPA UN 2015
Pembahasan Matematika IPA UN 2017
Pembahasan Matematika IPA UN 2018
Pembahasan Matematika IPA UN 2019
Pembahasan Matematika IPA UN 2019 Paket 2
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
