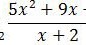pembahasan selanjutnya adalah
- limit fungsi,
- turunan fungsi,
- fungsi naik atau turun,
- aplikasi turunan, dan
- integral tak tentu.
Soal No. 26 tentang Limit Fungsi
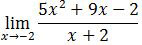
adalah ….
A. −11
B. −1
C. 0
D. 9
E. 11
Pembahasan
Ada dua cara menyelesaikan limit fungsi di atas, yaitu cara pemfaktoran dan penurunan.
Cara Pemfaktoran
Pembilang yang berbentuk fungsi kuadrat difaktorkan.
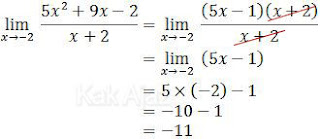
Cara Penurunan
Pembilang dan penyebut masing-masing diturunkan.
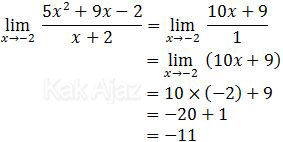
Jadi, nilai dari limit fungsi tersebut adalah −11 (A).
Soal No. 27 tentang Turunan Fungsi
A. f’ (x) = 18x(3x2 + 1)2
B. f’ (x) = 18x(3x2 + 1)3
C. f’ (x) = 3x(3x2 + 1)2
D. f’ (x) = 3x(3x2 + 1)3
E. f’ (x) = 6x(3x2 + 1)2

Pembahasan
Turunan di atas adalah turunan berantai. Caranya, fungsi yang ada di dalam kurung diturunkan terlebih dahulu. Setelah itu, secara keseluruhan (fungsi pangkat 3) diturunkan.
f(x) = (3x2 + 1)3
f’ (x) = 6x∙3(3x2 + 1)2
=18x(3x2 + 1)2
Jadi, turunan pertama fungsi f(x) adalah f’ (x) = 18x(3x2 + 1)2 (A).
Soal No. 28 tentang Fungsi Naik atau Turun
A. {x│−3 < x < 2, x ∈ R}
B. {x│−2 < x < 3, x ∈ R}
C. {x│x < −3 atau x > 2, x ∈ R}
D. {x│x < −2 atau x > 3, x ∈ R}
E. {x│x < −3 atau x > −2, x ∈ R}
Pembahasan
Suatu fungsi akan turun bila turunan fungsi tersebut bernilai negatif.
f(x) = ⅔ x3 − x2 − 12x + 12
f’ (x) < 0
2x2 − 2x − 12 < 0
x2 − x − 6 < 0
(x − 3)(x + 2) < 0
x = 3 dan x = −2
Karena tanda pertidaksamaannya maka intervalnya berada di antara x = −2 dan x = 3.
−2 < x < 3
Jadi, fungsi f(x) turun pada interval {x│−2 < x < 3, x ∈ R} (B).
Soal No. 29 tentang Aplikasi Turunan
A. 12.000 unit
B. 17.000 unit
C. 26.000 unit
D. 78.000 unit
E. 104.000 unit
Pembahasan
Biaya total untuk n unit:
B(n) = 10.000 + 8.000n + 1/3 n2
Harga jual n unit:
J(n) = 60.000 × n
Keuntungan n unit:
L(n) = J(n) − B(n)
= 60.000n − (10.000 + 8.000n + 1/3 n2 )
= −10.000 + 52.000n − 1/3 n2
Keuntungan maksimum untuk n unit:
L‘(n) = 0
52.000 − 2/3 n = 0
2/3 n = 52.000
n = 3/2 × 52.000
= 78.000
Jadi, keuntungan maksimum akan tercapai jika pakaian kemeja diproduksi sebanyak 78.000 unit (D).
Soal No. 30 tentang Integral Tak Tentu
A. x3 − 1/2 x2 − 6x + C
B. x3 + 7x2 + 6x + C
C. x3 + 1/2 x2 + 6x + C
D. x3 − 7/2 x2 − 6x + C
E. x3 − 7/2 x2 + 6x + C
Pembahasan
Dikatakan integral tak tentu karena hasil integralnya masih mengandung konstanta integrasi C.
∫(3x2 − 7x − 6) dx
= 3∙1/3 x3 − 7∙1/2 x2 − 6x + C
= x3 − 7/2 x2 − 6x + C
Jadi, hasil integral fungsi tersebut adalah x3 − 7/2 x2 − 6x + C (D).
Simak Pembahasan Soal Matematika IPS UN 2016 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat