pembahasan selanjutnya adalah
- luas permukaan bangun ruang,
- segitiga sebangun,
- kesebangunan,
- volume bangun ruang,
- ukuran pemusatan [modus].
Soal No. 31 tentang Luas Permukaan Bangun Ruang
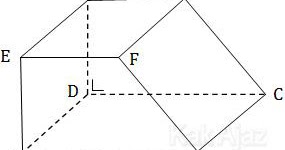
Panjang EF = 8 cm, AB = 16 cm, AE = 15 cm, dab BC = 9 cm. Luas permukaan prisma adalah ….
A. 864 cm2
B. 900 cm2
C. 1.100 cm2
D. 1.200 cm2
Pembahasan
Yang perlu diperhatikan adalah sisi-sisi trapesium ABFE.

Panjang FB harus kita ketahui untuk menentukan luas BCGF.
FB = √(82 + 152)
= √(64 + 225)
= √289
= 17
Sedangkan untuk menentukan luas trapesium ABFE kita gunakan rumus:
L.ABFE = ½ (AB + EF) × AE
= ½ (16 + 8) ×15
= 180
Dengan demikian, luas seluruh permukaan prisma trapesium tersebut adalah sebagai berikut:
L = 2×L.ABFE + L.ABCD + L.BCGF + L.EFGH + L.ADHE
= 2×180 + 16×9 + 9×17 + 8×9 + 15×9
= 360 + 144 + 153 + 72 + 135
= 864
Jadi, luas permukaan prisma tersebut adalah 864 cm2 (A).
Soal No. 32 tentang Segitiga Sebangun
Andi ingin mengetahui lebar sungai. Di samping sungai terdapat sebuah pohon. Untuk itu dia menancapkan tongkat pada posisi A, B, C, dan D dengan ukuran seperti pada gambar.
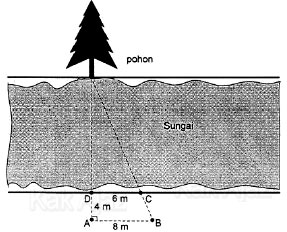
Andi ingin mengukur lebar sungai dari tongkat D sampai pohon. Berapa lebar sungai tersebut?
A. 11 m.
B. 12 m.
C. 15 m.
D. 16 m.

Pembahasan
Perhatikan sketsa berikut ini!

Segitiga ABP sebangun dengan segitiga DCP sehingga berlaku hubungan:
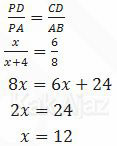
Jadi, lebar sungai tersebut adalah 12 m (B).
Soal No. 33 tentang Kesebangunan
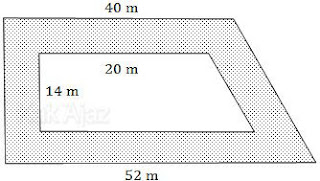
Sebidang lahan berbentuk trapesium siku-siku. Di dalam lahan terdapat kebun kelapa dan di sekeliling kebun akan dibuat jalan. Jika lahan dan kebun sebangun maka luas jalan tersebut adalah ….
A. 1.288 m2
B. 966 m2
C. 784 m2
D. 502 m2
Pembahasan
Perhatikan trapesium siku-siku berikut ini!

Kita tentukan dulu nilai x dan y dengan prinsip kesebangunan.

Selanjutnya, kita tentukan luas trapesium.
L = ½ × (jumlah sisi sejajar) × tinggi
Anggap saja luas trapesium yang besar L1.
L1 = ½ × (40 + 52) × 28
= ½ × 92 ×2 8
= 1288
Sedangkan trapesium yang kecil adalah L2.
L2 = ½ (20 + 26) × 14
= ½ × 46 × 14
= 322
Luas daerah yang diarsir adalah luas trapesium besar dikurangi luas trapesium kecil.
L = L1 − L2
= 1288 − 322
= 966
Jadi, luas jalan (bagian yang diarsir) tersebut adalah 966 m2 (B).
Soal No. 34 tentang Volume Bangun Ruang
A. 120 dm3
B. 240 dm3
C. 360 dm3
D. 720 dm3
Pembahasan
Perhatikan rumus volume kerucut berikut ini!
V = ⅓ πr2t
Diameter diperbesar 2 kali juga berarti jari-jari diperbesar 2 kali.
rb = 2r
tb = 3t
Sehingga volume kerucut setelah diperbesar adalah:
Vb = ⅓ π rb2 tb
= ⅓ π (2r)2 (3t)
= ⅓ π × 4r2 × 3t
= 12 × ⅓ πr2t
= 12 × V
= 12 × 20
= 240
Jadi, volume kerucut yang baru adalah 240 dm3 (B).
Soal No. 35 Ukuran Pemusatan [Modus]
20, 15, 19, 20, 18, 17, 17, 25, 19, 17, 17, 18, 15, 15, 23, 13.
Modus dan rata-rata berat badan balita tersebut berturut-turut adalah ….
A. 17 dan 18
B. 17 dan 19
C. 18 dan 17
D. 22 dan 18
Pembahasan
Modus adalah nilai yang sering muncul. Pada data di atas, berat badan 17 kg muncul 4 kali, data yang lain di bawah 4 kali. Sehingga modusnya adalah 17.
Sedangkan rata-rata adalah jumlah seluruh data dibandingkan dengan banyaknya data.

Jadi, Modus dan rata-rata berat badan balita tersebut berturut-turut adalah 17 dan 18 (A).
Simak Pembahasan Soal Matematika SMP UN 2016 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat