pembahasan selanjutnya adalah
- geometri,
- segitiga trigonometri,
- persamaan trigonometri,
- transformasi geometri, dan
- dimensi tiga.
Soal No. 1 tentang Geometri

Garis CE menyinggung lingkaran di titik F. Panjang CE = ….
A. 9√2
B. 13
C. 15
D. 9√3
E. 16
Pembahasan
Konsep dasar untuk memahami soal ini adalah:
Garis singgung lingkaran selalu tegak lurus dengan jari-jari lingkaran.
Perhatikan gambar di bawah ini!

Pandang layang-layang OBCF!
CB dan CF adalah garis singgung lingkaran. Karena keduanya berangkat dari titik yang sama maka panjang keduanya juga sama.
CF = CB = 12
Pandang layang-layang OAEF!
EA dan EF adalah garis singgung lingkaran. Anggap saja panjang EF = x, maka:
EA = EF = x
Sehingga panjang CE adalah:
CE = CF + EF
= 12 + x
Nah, kita tinggal menentukan nilai x.
Sekarang pandang segitiga CDE! Segitiga CDE adalah segitiga siku-siku sehingga berlaku teorema Pythagoras.
CE2 = CD2 + DE2
(12 + x)2 = 122 + (12 − x)2144 + 24x + x2 = 144 + 144 − 24x + x2
48x = 144
x = 3
Dengan demikian,
CE = 12 + x
= 12 + 3
= 15
Jadi, panjang CE adalah 15 (C).
Soal No. 2 tentang Segitiga Trigonometri
A. 15°
B. 20°
C. 30°
D. 45°
E. 50°

Pembahasan
Pertama yang harus dipahami adalah maksud dari CD = 2BD.
Variabel a di atas hanya permisalan. Anda bisa menggunakan variabel x, y, atau yang lain.
Perhatikan ilustrasi untuk soal di atas!

Padang segitiga ABD!
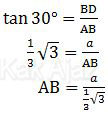
Dengan mengalikan pembilang dan penyebutnya dengan √3, diperoleh:
AB = a√3
Sekarang padang segitiga ABC!
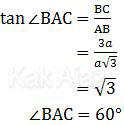
Dengan demikian ∠CAD adalah:
∠CAD = ∠BAC − ∠DAB
= 60° − 30°
= 30°
Jadi, sudut CAD adalah 30° (C).
Soal No. 3 tentang Persamaan Trigonometri
A. 2
B. 3
C. 4
D. 5
E. 6
Pembahasan
Mungkin yang agak asing adalah fungsi csc t. Apa itu csc t?
csc t = cosec t
= 1/(sin t)
Sehingga persamaan trigonometri di atas dapat diubah menunjukkan:
2 sin2 t − 2 sin t = 1 − csc t
2 sin2 t − 2 sin t = 1 − 1/(sin t)
Kalikan masing-masing suku dengan sin t.
2 sin3 t − 2 sin2 t = sin t − 1
2 sin3 t − 2 sin2 t − sin t + 1 = 0
Ternyata membentuk suku banyak berderajat tiga. Sebaiknya kita selesaikan dengan cara Horner.

Berdasarkan metode di atas diperoleh:
sin t = 1
t = 90°
Hasil bagi dari cara Horner tersebut (warna biru) adalah:
2 0 −1 yang berarti:
2 sin2 t − 1 = 0
2 sin2 t = 1
sin2 t = ½
sin t = ±½√2
Sampai di sini sebenarnya jawaban sudah bisa ditebak.
Coba perhatikan! Untuk interval 0 < t < 2π, sin t = 1 hanya ada 1 nilai, sin t = ½√2 dan sin t = −½√2 masing-masing mempunyai 2 nilai. Sehingga total nilai t adalah 5.
Baiklah, agar pembahasan lebih panjang, kita selesaikan satu per satu.
sin t = ½√2 (ada di kuadran I dan II)
t1 = 45°
t2 = (180 − 45)°
= 135°
sin t = −½√2 (ada di kuadran III dan IV)
t1 = (180 + 45)°
= 225°
t2 = (360 − 45)°
= 315°
Dengan demikian himpunan penyelesaian persamaan trigonometri tersebut adalah:
{45°, 90°, 135°, 225°, 315°}
Jadi, banyaknya anggota himpunan penyelesaian dari persamaan di atas adalah 5 (D).
Soal No. 4 tentang Transformasi Geometri
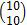 maka a + b = ….
maka a + b = ….
A. s + t + 20
B. 2s + t + 10
C. s + t + 10
D. s + 2t + 10
E. s + t + 5
Pembahasan
Pencerminan titik P(x, y) terhadap garis x = h dan y = k masing dirumuskan sebagai:

Berpedoman pada rumus di atas, pencerminan titik P(s, t) terhadap garis x = a adalah:

Hasil dari pencerminan tersebut dicerminkan lagi terhadap garis y = b. Diperoleh:
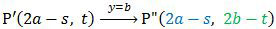
Hasil pencerminan yang terakhir ini sama dengan translasi 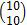 terhadap titik P(s, t).
terhadap titik P(s, t).
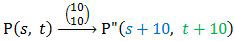
Sehingga diperoleh hubungan:
2a − s = s + 10
2a = 2s + 10
a = s + 5
2b − t = t + 10
2b = 2t + 10
b = t + 5
Dengan demikian,
a + b = (s + 5) + (t + 5)
= s + t + 10
Jadi, nilai dari a + b adalah s + t + 10 (C).
Soal No. 5 tentang Dimensi Tiga
A. 5/44 √44
B. 5/33 √33
C. 5/22 √22
D. 1/13 √13
E. 1/11 √11
Pembahasan
Gambaran kubus yang dimaksud adalah sebagai berikut:

Anggap saja rusuk kubus tersebut adalah 3a (untuk mempermudah penghitungan) sehingga:
AM = CN = PH = a
MD = ND = DP = 2a
Segitiga MNP adalah segitiga sama sisi dengan panjang rusuk (pandang segitiga MDP):
MP = √(MD2 + DP2)
= √[(2a)2 + (2a)2]
= 2a√2
PQ adalah tinggi segitiga sama sisi MNP. Tinggi segitiga sama sisi dirumuskan:
t = ½√3 × rusuk segitiga
PQ = ½√3 × 2a√2
= a√6
BD adalah diagonal alas kubus yang dirumuskan:
BD = rusuk kubus × √2
= 3a√2
Sedangkan BQ adalah 2/3 diagonal.
BQ = 2/3 × 3a√2
= 2a√2
Sekarang tinggal menentukan panjang BP. Pandang segitiga BDP!
BP = √(BD2 + DP2 )
= √[(3a√2)2 + (2a)2]
= √(18a2 + 4a2 )
= a√22
Nah, semua rusuk segitiga BPQ sudah diketahui yang mana sudut α ada di dalamnya.

Kita gunakan aturan kosinus untuk mendapatkan nilai dari cos α.
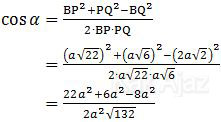
Variabel a2 bisa dicoret dan √132 = 2√33, sehingga diperoleh:

Jadi, nilai cos α adalah 5/33 √33 (B).
Simak Pembahasan Soal TKD Saintek SBMPTN 2016 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
