pembahasan selanjutnya adalah
- suku banyak,
- fungsi eksponen,
- limit fungsi,
- barisan dan deret, serta
- titik stasioner dan nilai ekstrem.
Soal No. 6 tentang Suku Banyak
A. 5/2
B. 5/4
C. 1/4
D. 1
E. 4
Pembahasan
Mari kita pahami kembali teorema sisa berikut ini!
Jika f(x) dibagi oleh x − a
maka sisanya adalah f(a)
Berdasarkan teorema sisa tersebut, sisa pembagian (f(x))2 + (g(x))2 oleh x − 1 adalah:
(f(1))2 + (g(1))2
Itulah yang ditanyakan. Berarti kita tinggal mencari nilai dari f(1) dan g(1).
Mari kita perhatikan pernyataan pada soal di atas!
Sisa pembagian suku banyak f(x) − g(x) oleh x2 + x − 2 adalah x.
Pembagi suku banyak tersebut berbentuk kuadrat yang dapat difaktorkan menjadi:
x2 + x − 2 = (x + 2)(x − 1)
Artinya, jika f(x) − g(x) dibagi x2 + x − 2 bersisa x, maka dibagi (x + 2) atau (x − 1) pun juga akan bersisa x.
Karena kita butuh nilai f(1) dan g(1) maka kita gunakan pembagi (x − 1). Sehingga sisa pembagian ini adalah:
f(1) − g(1) = 1 … (1)
Sekarang kita perhatikan pernyataan berikutnya.
Sisa pembagian f(x) + g(x) oleh x2 − 3x + 2 adalah x + 1.
Faktor pembaginya adalah:
x2 − 3x + 2 = (x − 1)(x − 2)
Kita gunakan faktor pembagi (x − 1) sehingga sisa pembagian ini adalah:
f(1) + g(1) = 1 + 1
f(1) + g(1) = 2 … (2)
Nah, sekarang kita eliminasi persamaan (1) dan (2).
f(1) − g(1) = 1
f(1) + g(1) = 2
⎯⎯⎯⎯⎯⎯⎯⎯⎯ +
2f(1) = 3
f(1) = 3/2
Substitusi f(1) = 3/2 ke persamaan (2).
f(1) + g(1) = 2
3/2 + g(1) = 2
g(1) = 1/2
Dengan demikian,
(f(1))2 + (g(1))2 = (3/2)2 + (1/2)2
= 9/4 + 1/4
= 10/4
= 5/2
Jadi, sisa pembagian (f(x))2 + (g(x))2 oleh x − 1 adalah 5/2 (A).
Soal No. 7 tentang Fungsi Eksponen
A. 0 < x < 1
B. x > 1
C. x < 0
D. x > 3
E. 1 < x < 3

Pembahasan
Misalkan:
y1 = 3x+1 − (1/9)x
= 3 . 3x − 3−2x
y2 = 3x + 1
Karena y1 berada di bawah y2 maka nilai y1 kurang dari y2.
y1 < y2
3 . 3x − 3−2x < 3x + 1
Agar lebih enak dipandang, kita misalkan p = 3x. diperoleh:
3p − p−2 < p + 1
2p − p−2 − 1 < 0
Selanjutnya, masing-masing suku kita kalikan dengan p2, tujuannya supaya tidak mengandung pangkat negatif.
2p3 − 1 − p2 < 0
2p3 − p2 − 1 < 0
Bentuk terakhir ini adalah suku banyak berderajat tiga. Penyelesaiannya bisa dengan cara Horner seperti soal no. 3 di atas.
Bisa juga dengan memperhatikan koefisiennya. Karena jumlah semua koefisiennya sama dengan nol maka dapat dipastikan salah satu faktornya adalah (p − 1). Sehingga bentuk di atas bisa diubah menjadi:
(p − 1)(2p2 + p + 1) < 0
Faktor kedua, yaitu 2p2 + p + 1, ternyata tidak dapat difaktorkan lagi. Berarti definit positif sehingga dapat diabaikan.
p − 1 < 0
p < 1
Sekarang kita kembalikan nilai p = 3x.
3x < 1
3x < 3
x < 0
Jadi, y1 berada di bawah y1 jika x < 0 (C).
Soal No. 8 tentang Limit Fungsi
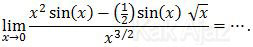
A. −∞
B. −7/2
C. −5/2
D. −3/2
E. −1/2
Pembahasan
Limit fungsi trigonometri mendekati nol berlaku hubungan:
x = sin x = tan x
Dengan memanfaatkan hubungan tersebut, mari kita ganti sin x pada soal di atas dengan x.
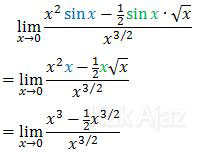
Masing-masing suku dibagi x3/2, diperoleh:
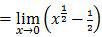
Nah, sekarang tinggal memasukkan x = 0.
= 0 − 1/2
= −1/2
Jadi, nilai dari limit fungsi tersebut adalah −1/2 (E).
Soal No. 9 tentang Barisan dan Deret
A. −2
B. −1
C. 0
D. 1
E. 2
Pembahasan
an yang dimaksud pada soal adalah suku ke-n barisan geometri yang dirumuskan:
an = arn−1
Berpedoman pada rumus tersebut maka:
a2 + a5 − a4 = 10
ar + ar4 − ar3 = 10 … (1)
a3 + a6 − a5 = 20
ar2 + ar5 − ar4 = 20 … (2)
Mari kita bandingkan persamaan (1) dan (2)!
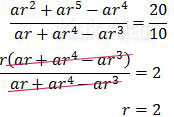
Substitusi r = 2 ke persamaan (1).
ar + ar4 − ar3 = 10
2a + 16a − 8a = 10
10a = 10
a = 1
Dengan demikian,
a2 = ar
= 1×2
= 2
Jadi, nilai dari a2 adalah 2 (E).
Soal No. 10 tentang Titik Stasioner dan Nilai Ekstrem
A. 10
B. 8
C. 6
D. 4
E. 3
Pembahasan
f(x) memotong sumbu y di titik (0, 10) artinya f(0) = 10.
f(x) = x3 − 3x2 + a
f(0) = 03 − 3.2 + a
10 = a
Sehingga fungsi lengkap dari f(x) adalah:
f(x) = x3 − 3x2 + 10
Fungsi f(x) akan mencapai nilai minimum apabila turunan fungsi tersebut sama dengan nol.
f’(x) = 0
3x2 − 6x = 0
x2 − 2x = 0
x(x − 2) = 0
x = 0 atau x = 2
Karena x ∈ [0, 1] maka x = 2 tidak memenuhi.
Selanjutnya kita cari nilai dari f(0) dan f(1) untuk menentukan nilai minimumnya.
f(x) = x3 − 3x2 + 10
f(0) = 0 − 0 + 10
= 10 (maksimum)
f(1) = 1 − 3 + 10
= 8 (minimum)
Jadi, nilai minimum f(x) untuk x ∈ [0, 1] adalah 8 (B).
Simak Pembahasan Soal TKD Saintek SBMPTN 2016 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
