pembahasan selanjutnya adalah

Pembahasan soal Matematika Tes Kemampuan Dasar Sains dan Teknologi (TKD Saintek) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2017 Kode Naskah 157 nomor 11 sampai dengan nomor 15 tentang:
- limit fungsi trigonometri,
- fungsi rasional,
- turunan fungsi,
- persamaan garis, dan
- teori peluang.
Soal No. 11 tentang Limit Fungsi Trigonometri

A. −3/4
B. 1/2
C. 3/4
D. 4/3
E. 2
Pembahasan
Limit fungsi trigonometri di atas dapat kita selesaikan dengan mudah apabila kita ubah batas nilai limitnya dari ∞ menjadi 0 sebagai berikut:
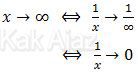
Sehingga
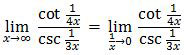
Nah, sekarang kita tinggal mengubah cot x menjadi 1/(tan x) dan csc x menjadi 1/(sin x).

Untuk limit fungsi trigonometri mendekati berlaku tan x = sin x sehingga diperoleh:

Jadi, nilai dari limit fungsi trigonometri tersebut adalah 4/3 (D).
Soal No. 12 tentang Fungsi Rasional
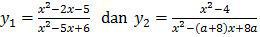
Jika diketahui salah satu asimtot tegak dari y1 dan y2 berjarak 4 satuan maka a = ….
A. 7
B. 8
C. 9
D. 10
E. 11

Pembahasan
Asimtot tegak suatu fungsi pecahan terjadi saat penyebut pecahan tersebut sama dengan nol.
Dengan demikian, asimtot tegak fungsi y1 adalah:
x2 − 5x + 6 = 0
(x − 2)(x − 3) = 0
x = 2 atau x = 3
Sedangkan asimtot tegak fungsi y2 adalah:
x2 − (a + 8)x + 8a = 0
(x − a)(x − 8) = 0
x = a atau x = 8
Sementara itu, jarak salah satu asimtot tegak fungsi y1 dan y2 dari a adalah 4.
a − 2 = 4
a = 6
a − 3 = 4
a = 7
Jadi, sesuai dengan opsi jawaban yang ada, nilai a adalah 7 (A).
Soal No. 13 tentang Turunan Fungsi
A. −2 sin x cos(cos2 x)
B. −2 sin 2x cos(cos2 x)
C. −sin x cos(cos2 x)
D. −sin 2x cos(cos2 x)
E. −sin2 x cos(cos2 x)
Pembahasan
Perhatikan fungsi f(x)!
f(x) = sin(cos2 x)
Misalkan:
cos x = v → dv/dx = −sin x
cos2 x = v2 = u → du/dv = 2v
sin(cos2 x) = sin u → df/du = cos u
Dengan demikian,
f ‘(x) = df/dx
= df/du ∙ du/dv ∙ dv/dx
= cos u ∙ 2v ∙ (−sin x)
= cos(cos2 x) ∙ 2cos x ∙ (−sin x)
= −2sin x cos x cos(cos2 x)
Mengingat rumus sin 2x = 2sin x cos x, diperoleh:
= −sin 2x cos(cos2 x)
Jadi, turunan dari fungsi f(x) adalah opsi (D).
Soal No. 14 tentang Persamaan Garis
A. −2a − 1
B. 1
C. 2a + 1
D. −1
E. −a − 1
Pembahasan
Gradien garis singgung f(x) berpotongan dengan garis y = x − 1 di titik (b, c). Artinya, garis y = x − 1 melalui titik (b, c).
Oleh karena itu, kita bisa langsung melakukan substitusi titik (b, c) terhadap garis y = x − 1.
(b, c) → y = x − 1.
c = b − 1
c − b = −1
b − c = 1
Jadi, nilai dari b − c adalah 1 (B).
Soal No. 15 tentang Teori Peluang
A. 0,04
B. 0,10
C. 0,16
D. 0,32
E. 0,40
Pembahasan
Diketahui:
Kotak I : 12 bola putih + 3 merah (15 bola)
Kotak II : 4 bola putih + 4 merah (8 bola)
Jika tiap kotak diambil 2 bola dengan pengembalian maka kemungkinan terambilnya 1 bola merah:
Kota I terambil 1 bola merah dan 1 bola putih sedangkan kotak II terambil 2 bola putih.
MP dan PP : 3/15 × 12/15 × 4/8 × 4/8 = 1/25
PM dan PP : 12/15 × 3/15 × 4/8 × 4/8 = 1/25
Kota I terambil 2 bola putih dan kotak II terambil 1 bola merah dan 1 bola putih.
PP dan MP : 12/15 × 12/15 × 4/8 × 4/8 = 4 /25
PP dan PM : 12/15 × 12/15 × 4/8 × 4/8 = 4/25
Dengan demikian, peluang terambilnya 1 bola merah dari kotak I dan II dengan masing-masing 2 pengambilan adalah:
1/25 + 1/25 + 4/25 + 4/25 = 10/25
= 0,4
Jadi, peluang yang terambil adalah 1 bola merah adalah 0,40 (E).
Simak Pembahasan Soal TKD Saintek SBMPTN 2017 selengkapnya.
Simak juga:
Pembahasan Matematika SBMPTN 2014
Pembahasan Matematika SBMPTN 2015
Pembahasan Matematika SBMPTN 2016
Pembahasan Matematika SBMPTN 2018
Pembahasan Matematika UTBK SBMPTN 2019
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
