pembahasan selanjutnya adalah

Pembahasan soal-soal Ujian Nasional (UN) tahun 2017 bidang studi Matematika SMA-IPA nomor 11 sampai dengan nomor 15 tentang:
- operasi matriks,
- invers matriks,
- sistem persamaan linear,
- program linear (nilai maksimum),
- program linear (prosentase maksimum).
Soal No. 11 tentang Operasi Matriks

Jika A + B = CD maka a + b + c = ….
A. −6
B. −2
C. 0
D. 6
E. 8
Pembahasan
Matriks termasuk materi yang mudah tetapi membutuhkan ketelitian. Mari kita kerjakan pelan-pelan!

Nah, sudah terbentuk kesamaan matriks. Berarti komponen yang bersesuaian mempunyai nilai yang sama.
4 − a = 8
−a = 4
a = −4
b + 5 = 6
b = 1
−2c − 4 = −10
−2c = −6
c = 3
Dengan demikian,
a + b + c = −4 + 1 + 3
= 0
Jadi, nilai dari a + b + c adalah 0 (C).
Perdalam materi ini di Pembahasan Matematika IPA UN: Matriks.
Soal No. 12 tentang Invers Matriks
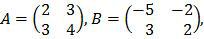
dan matriks AB = C. Matriks C−1 adalah invers matriks C, maka matriks C−1 = ….


Pembahasan
Kita operasikan matriks A kali matriks B untuk mendapatkan matriks C.

Selanjutnya kita tentukan invers matriks C dengan menggunakan rumus:
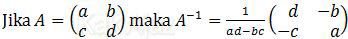
Sehingga,

Jadi, invers dari matriks C adalah opsi (A).
Perdalam materi ini di Pembahasan Matematika IPA UN: Matriks.
Soal No. 13 tentang Sistem Persamaan Linear
A. Rp23.000,00
B. Rp24.000,00
C. Rp25.000,00
D. Rp27.000,00
E. Rp33.000,00
Pembahasan
Misalkan x, y, dan z secara berurutan mewakili buku tulis, pensil, dan penggaris maka model matematikanya adalah:
Dira : 2x + y + z = 19.000 … (1)
Anita : x + 2y + 2z = 20.000 … (2)
Sita : 3x + 2y + z = 28.000 … (3)
Eliminasi persamaan (1) dan (2) dengan mengalikan 2 pada persamaan (1) terlebih dahulu.
4x + 2y + 2z = 38.000
x + 2y + 2z = 20.000
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ −
3x = 18.000
x = 6.000
Selanjutnya, eliminasi persamaan (3) dan (1)
3x + 2y + z = 28.000
2x + y + z = 19.000
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ −
x + y = 9.000
6.000 + y = 9.000
y = 3.000
Kemudian kita substitusikan nilai x dan y pada persamaan (1).
2x + y + z = 19.000
2×6.000 + 3.000 + z = 19.000
z = 4.000
Dengan demikian, harga 1 buku tulis, 3 pensil, dan 2 penggaris adalah:
x + 3y + 2z = 6.000 + 3×3.000 + 2×4.000
= 6.000 + 9.000 + 8.000
= 23.000
Jadi, harga 1 buku tulis, 3 pensil, dan 2 penggaris adalah Rp23.000,00 (A).
Perdalam materi ini di Pembahasan Matematika IPA UN: Sistem Persamaan dan Pertidaksamaan Linear.
Soal No. 14 tentang Program linear (Nilai Maksimum)
A. Rp22.500.000,00
B. Rp21.000.000,00
C. Rp20.000.000,00
D. Rp15.000.000,00
E. Rp9.000.000,00
Pembahasan
Berikut ini tabel bantuan untuk soal di atas.
| Model A (x) | Model B (y) | ||
| Biaya | 3 |
4 |
55 |
| Waktu | 2 | 5 | 60 |
| Untung | 1.000.000 | 1.500.000 |
Berdasarkan tabel bantuan di atas, kita dapat membuat model matematika sebagai berikut:
3x + 4y = 55 … (1)
2x + 5y = 60 … (2)
Fungsi sasaran: U(x, y) = 1.000.000x + 1.500.000y
Sekarang kita eliminasi persamaan (1) dan (2). Sebelumnya persamaan (1) kita kalikan 2 sedangkan persamaan (2) kita kalikan 3. Diperoleh:
6x + 8y = 110
6x + 15y = 180
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ − (bawah dikurangi atas)
7y = 70
y = 10
Kemudian y = 10 kita substitusikan ke persamaan (1) untuk mendapatkan nilai x.
3x + 4y = 55
3x + 40 = 55
3x = 15
x = 5
Dengan demikian, keuntungan maksimum tercapai ketika x = 5 dan y = 10.
U(x, y) = 1.000.000x + 1.500.000y
U(5, 10) = 1.000.000×5 + 1.500.000×10
= 5.000.000 + 15.000.000
= 20.000.000
Jadi, keuntungan maksimum yang dapat diperoleh adalah Rp20.000.000,00 (C).
Perdalam materi ini di Pembahasan Matematika IPA UN: Program Linear.
Soal No. 15 tentang Program Linear (Persentase Maksimum)
A. 30%
B. 34%
C. 36%
D. 38%
E. 40%
Pembahasan
Tabel bantuan untuk soal di atas adalah sebagai berikut:
| Model I (x) | Model II (y) | 40 | |
| Biaya | 2 |
3 |
100 |
| Untung | 40% × 20.000 = 8.000 |
30% × 30.000 = 9.000 |
Berdasarkan tabel bantuan di atas, diperoleh model matematika:
x + y = 40 … (1)
2x + 3y = 100 … (2)
Fungsi objektif: U(x, y) = 8.000x + 9.000y
Eliminasi persamaan (1) dan (2) dengan mengalikan persamaan (1) dengan 2 terlebih dahulu.
2x + 2y = 80
2x + 3y = 100
⎯⎯⎯⎯⎯⎯⎯⎯⎯ − (bawah dikurangi atas)
y = 20 → x = 20
Dengan demikian, pengrajin tersebut akan memperoleh keuntungan maksimum saat x = y = 20.
U(x, y) = 8.000x + 9.000y
U(20, 20) = 8.000×20 + 9.000×20
= 160.000 + 180.000
= 340.000
Persentase keuntungan terhadap modal adalah:
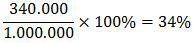
Jadi, persentase keuntungan terbesar yang dapat dicapai pengrajin tas tersebut adalah 34% (B).
Perdalam materi ini di Pembahasan Matematika IPA UN: Program Linear.
Simak Pembahasan Soal Matematika IPA UN 2017 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
