pembahasan selanjutnya adalah

Pembahasan soal-soal Ujian Nasional (UN) tahun 2017 bidang studi Matematika SMA-IPS nomor 16 sampai dengan nomor 20 tentang:
- kesamaan matriks,
- determinan matriks,
- barisan dan deret aritmetika,
- barisan dan deret geometri, serta
- penerapan barisan geometri.
Soal No. 16 tentang Kesamaan Matriks

Jika A + B = CT dengan CT menyatakan transpos matriks C maka nilai a − 2b + c adalah ….
A. −8
B. −5
C. −2
D. 0
E. 5
Pembahasan
Transpos matriks C adalah baris dari matriks C yang menjadi kolom dari CT.
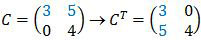
Mari kita operasikan persamaan matriks di atas agar menjadi kesamaan matriks.

Berdasarkan kesamaan matriks di atas diperoleh:
a + 4 = 0
a = −4
2b + 1 = 5
2b = 4
b = 2
c + 1 = 4
c = 3
Dengan demikian,
a − 2b + c = −4 − 2×2 + 3
= −4 − 4 + 3
= −5
Jadi, nilai dari a − 2b + c adalah −5 (B).
Soal No. 17 tentang Determinan Matriks
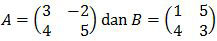
Determinan A × B adalah ….
A. −391
B. −119
C. −41
D. 41
E. 391

Pembahasan
Kita ingat dulu rumus determinan matriks.
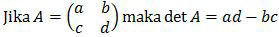
Kemudian kita ingat juga sifat determinan matriks, bahwa:
det(A×B) = det A × det B
Nah, sekarang kita cari determinan matriks A dan determinan matriks B.

Dengan demikian,
det(A×B) = det A × det B
= 23 × (−17)
= −391
Jadi, determinan A×B adalah −391 (A).
Soal No. 18 tentang Barisan dan Deret Aritmetika
A. 50
B. 55
C. 60
D. 65
E. 70
Pembahasan
Suku ke-n barisan aritmetika dirumuskan sebagai:
Un = a + (n − 1)b
Berdasarkan rumus tersebut diperoleh:
U5 = a + 4b = 4
U8 = a + 7b = 10
⎯⎯⎯⎯⎯⎯⎯⎯ −
−3b = −6
b = 2
Substitusi b = 2 pada U5 diperoleh:
a + 4b = 4
a + 4×2 = 4
a + 8 = 4
a = −4
Sedangkan untuk mendapatkan jumlah 10 suku pertama, kita gunakan rumus:
Sn = n/2 [2a + (n − 1)b]
U10 = 10/2 [2×(-4)+(10-1)2]
= 5(−8 + 18)
= 5×10
= 50
Jadi, jumlah sepuluh suku pertama deret tersebut adalah 50 (A).
Soal No. 19 tentang Barisan dan Deret Geometri
A. 1.024
B. 512
C. 256
D. 128
E. 64
Pembahasan
Rumus suku ke-n barisan geometri adalah:
Un = arn−1
Berpedoman pada rumus tersebut diperoleh:
U2 = ar = 4
U6 = ar5 = 64
Jika U6 dibagi dengan U2, diperoleh:

Nilai suku pertama a bisa dapatkan melalui U2.
ar = 4
a×2 = 4
a = 2
Dengan demikian, suku ke sepuluh deret tersebut adalah:
U10 = ar9
= 2×29
= 210
= 1024
Jadi, Suku ke-10 barisan tersebut adalah 1.024 (A).
Soal No. 20 tentang Penerapan Barisan Geometri
A. 256 orang
B. 512 orang
C. 1.280 orang
D. 2.560 orang
E. 5.204 orang
Pembahasan
Soal di atas sebenarnya mudah ditebak. Coba perhatikan! Tahun 2013 pertambahan penduduk 5 orang dan tahun 2015 pertambahannya 80 orang. Artinya, selama 2 tahun pertambahan penduduk naik 16 kali (80 : 5).
Dengan demikian, 2 tahun kemudian (tahun 2017) pertambahan penduduknya diperkirakan juga naik 16 kali sehingga menjadi 80×16 = 1280.
Ok, supaya lebih meyakinkan, kita selesaikan dengan menggunakan rumus deret geometri.
Tahun 2013 → a = 5
Tahun 2014 → U2
Tahun 2015 → U3 = 80
Tahun 2016 → U4
Tahun 2017 → U5 = ?
Pada barisan geometri berlaku rumus:
Un = arn−1
Sehingga:
U3 = ar2
80 = 5r2
r2 = 80/5
= 16
r = 4
Dengan demikian, suku ke-5 adalah:
U5 = ar4
= 5 × 44
= 5 × 256
= 1280
Jadi, pertambahan penduduk pada tahun 2017 adalah 1.280 orang (C).
Simak Pembahasan Soal Matematika IPS UN 2017 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
